Evaluate the integral from 0 to π/2 of (x sin(x)) / (1 + cos^2(x)) dx.
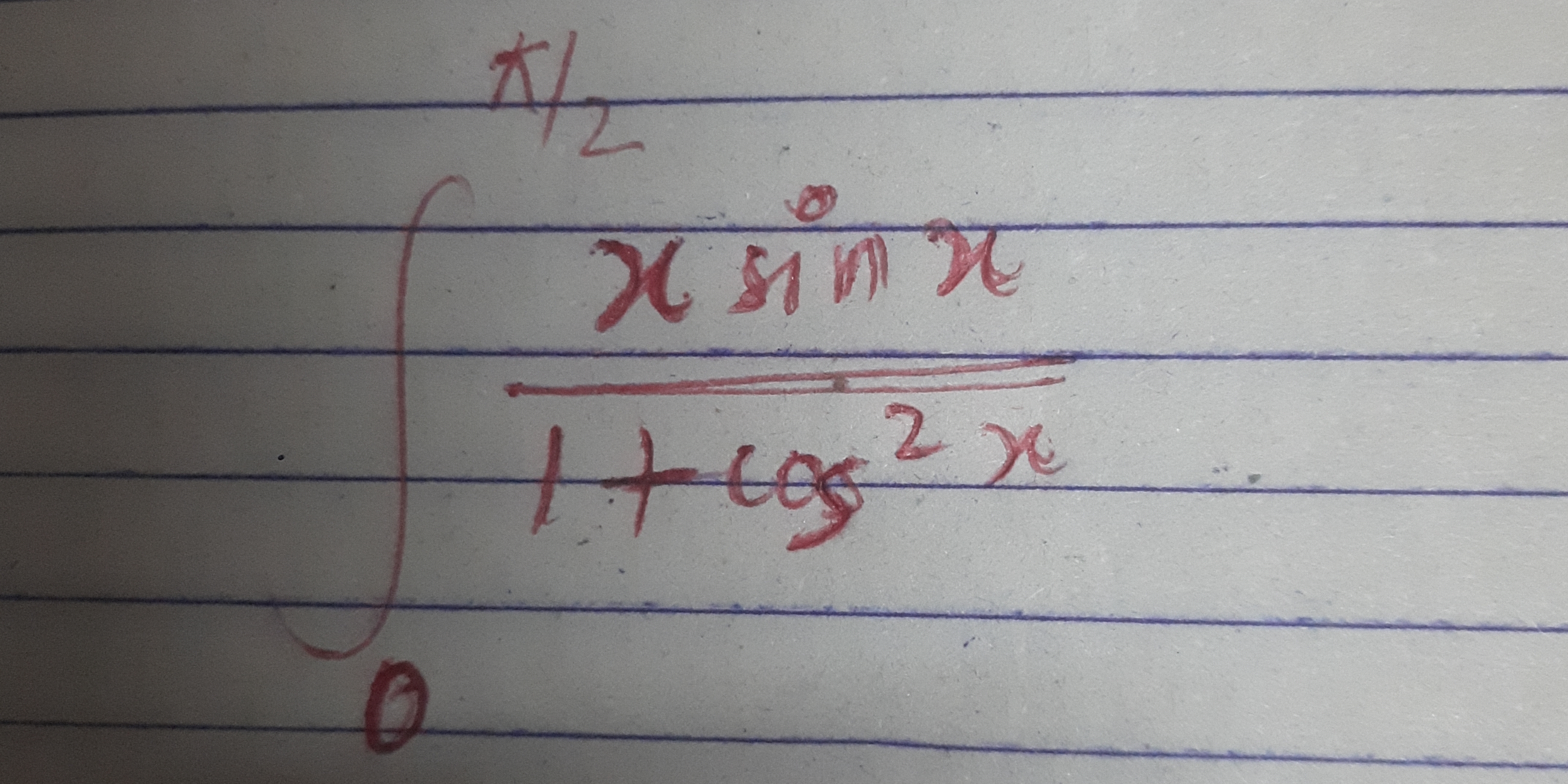
Understand the Problem
The question involves evaluating the integral of the function x sin(x) divided by (1 + cos^2(x)) from 0 to π/2. It is asking for the computation of this definite integral.
Answer
The integral evaluates to $I = \frac{\pi^2}{8}$.
Answer for screen readers
The value of the integral is: $$ I = \frac{\pi^2}{8} $$
Steps to Solve
-
Set up the integral We start with the integral we want to evaluate: $$ I = \int_0^{\frac{\pi}{2}} \frac{x \sin(x)}{1 + \cos^2(x)} , dx $$
-
Consider integration by parts To tackle this integral, we apply the technique of integration by parts. We let:
- ( u = x ) → then ( du = dx )
- ( dv = \frac{\sin(x)}{1 + \cos^2(x)} , dx )
- Compute ( v ) Next, we need to find ( v ). To do this, we integrate ( dv ). We can express ( v ) as: $$ v = \int \frac{\sin(x)}{1 + \cos^2(x)} , dx $$
Let ( w = \cos(x) ), then ( dw = -\sin(x) , dx ). The integral transforms to: $$ v = -\int \frac{1}{1 + w^2} , dw = -\tan^{-1}(w) + C = -\tan^{-1}(\cos(x)) + C $$
-
Apply integration by parts formula Now using the integration by parts formula ( \int u , dv = uv - \int v , du ), we substitute: $$ I = \left[-x \tan^{-1}(\cos(x))\right]_0^{\frac{\pi}{2}} + \int_0^{\frac{\pi}{2}} \tan^{-1}(\cos(x)) , dx $$
-
Evaluate boundary terms Evaluate the boundary term:
- At ( x = \frac{\pi}{2} ): ( -\frac{\pi}{2} \tan^{-1}(\cos(\frac{\pi}{2})) = -\frac{\pi}{2} \cdot 0 = 0 )
- At ( x = 0 ): ( -0 \cdot \tan^{-1}(\cos(0)) = -0 \cdot \frac{\pi}{4} = 0 )
Thus, the boundary term is 0, and we have: $$ I = \int_0^{\frac{\pi}{2}} \tan^{-1}(\cos(x)) , dx $$
- Final form of the integral Now, we've reduced our original integral to the evaluation of: $$ I = \int_0^{\frac{\pi}{2}} \tan^{-1}(\cos(x)) , dx $$
This integral can be evaluated using symmetry or known results.
The value of the integral is: $$ I = \frac{\pi^2}{8} $$
More Information
The integral ( \int_0^{\frac{\pi}{2}} \tan^{-1}(\cos(x)) , dx ) is a known result and is related to Fourier series and the evaluation of definite integrals involving trigonometric functions.
Tips
- Misapplying integration by parts; ensure you identify ( u ) and ( dv ) correctly.
- Forgetting to evaluate the boundary terms properly.
- Confusion between ( \tan^{-1} ) and ( \sin^{-1} ); remember their properties and ranges.
AI-generated content may contain errors. Please verify critical information