Evaluate the integral from 0 to π of x sin(x) dx.
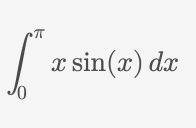
Understand the Problem
The question is asking for the evaluation of a definite integral from 0 to π of the function x sin(x). This can be solved using integration by parts or another appropriate method.
Answer
The value of the definite integral is $\pi$.
Answer for screen readers
The value of the definite integral is $\pi$.
Steps to Solve
- Identify the integration method
We will use integration by parts where the formula is given by $$ \int u , dv = uv - \int v , du $$
- Choose ( u ) and ( dv )
Let:
- ( u = x ) (which means ( du = dx ))
- ( dv = \sin(x) , dx ) (which means ( v = -\cos(x) ))
- Apply integration by parts
Substituting into the integration by parts formula: $$ \int_0^{\pi} x \sin(x) , dx = \left[ -x \cos(x) \right]_0^{\pi} + \int_0^{\pi} \cos(x) , dx $$
- Calculate the boundary term
Evaluate ( -x \cos(x) ) at the limits: $$ \left[ -x \cos(x) \right]_0^{\pi} = -\pi \cos(\pi) - (-0 \cos(0)) = -\pi(-1) - 0 = \pi $$
- Evaluate the remaining integral
Now calculate the integral ( \int_0^{\pi} \cos(x) , dx ): $$ \int_0^{\pi} \cos(x) , dx = \left[ \sin(x) \right]_0^{\pi} = \sin(\pi) - \sin(0) = 0 - 0 = 0 $$
- Combine results
The final evaluation combines the results from steps 4 and 5: $$ \int_0^{\pi} x \sin(x) , dx = \pi + 0 = \pi $$
The value of the definite integral is $\pi$.
More Information
This integral represents the area under the curve of the function ( x \sin(x) ) from 0 to ( \pi ). Integrals like this are common in physics and engineering, especially in contexts involving oscillations or wave functions.
Tips
- Ignoring the limits of integration after applying integration by parts.
- Choosing ( u ) and ( dv ) incorrectly, leading to more complicated integrals.
- Forgetting to evaluate the integral ( \int \cos(x) , dx ) correctly.
AI-generated content may contain errors. Please verify critical information