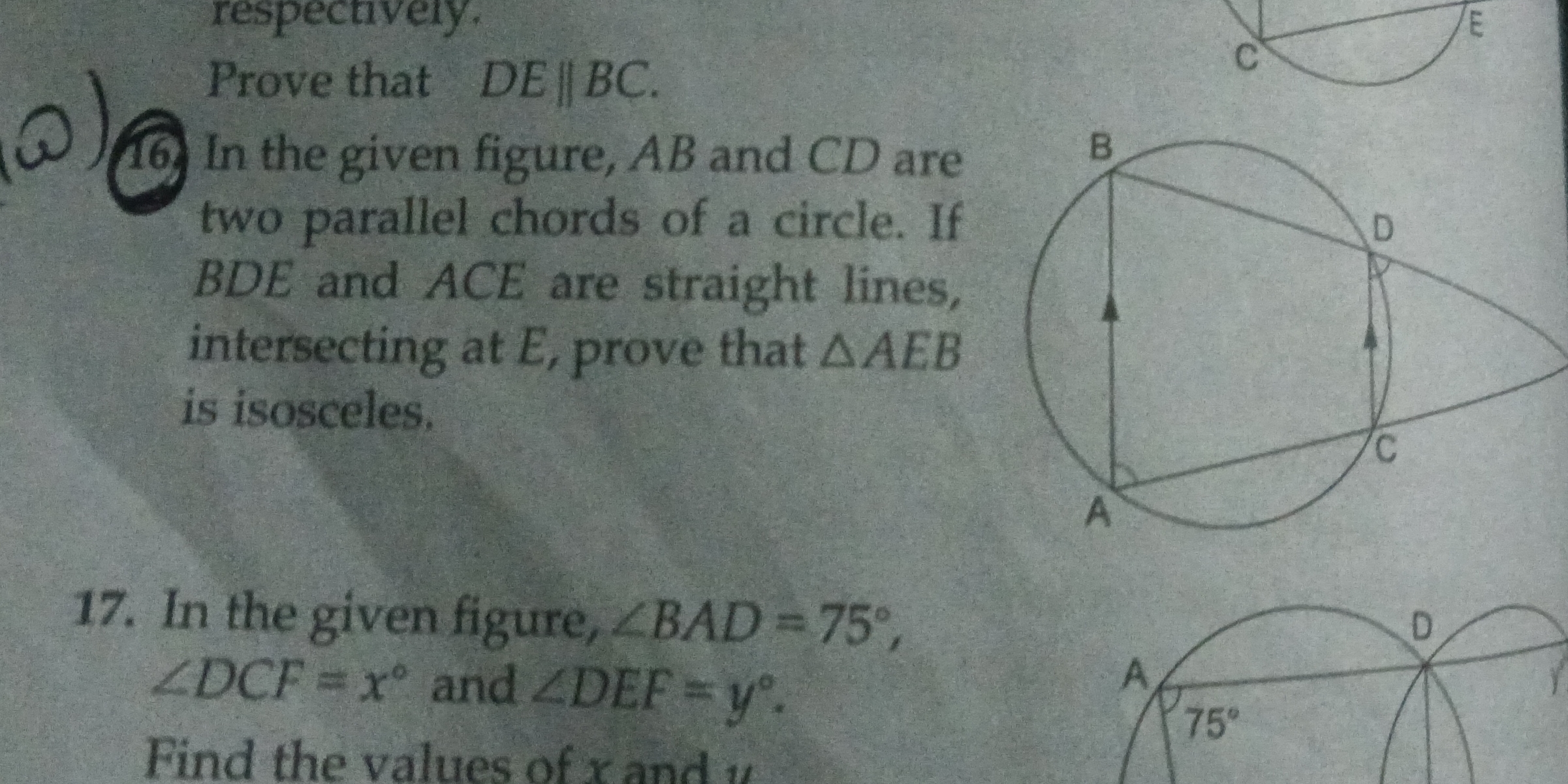
In the given figure, AB and CD are two parallel chords of a circle. If BDE and ACE are straight lines intersecting at E, prove that triangle AEB is isosceles.
Understand the Problem
The question is asking to prove that triangle AEB is isosceles based on the information provided about the chords AB and CD in the circle, along with the intersecting lines BDE and ACE. This involves understanding the properties of parallel lines and angles subtended by the same chord in a circle.
Answer
Triangle $AEB$ is isosceles.
Answer for screen readers
Triangle $AEB$ is isosceles.
Steps to Solve
-
Identify the Properties of Chords Since $AB$ and $CD$ are chords of a circle and are parallel, we know that angles subtended by the same chord at any point on the circle are equal.
-
Consider Angles at Intersection Point E At points B and D:
- Angle $ABE$ subtended by chord $AB$ at point $E$.
- Angle $CDE$ subtended by chord $CD$ at point $E$.
Since $AB$ || $CD$, we find: $$ \angle ABE = \angle CDE $$
- Apply Alternate Interior Angles Theorem Since $AB$ and $CD$ are parallel, we also have:
- Angle $ABE$ is equal to angle $AED$ (alternate interior angles).
Thus: $$ \angle ABE = \angle AED $$
- Conclude the Angles Are Equal Now we have: $$ \angle ABE = \angle AED $$ and $$ \angle ABE = \angle CDE $$
This implies $$ \angle AED = \angle CDE $$
- Establish Isosceles Triangle AEB Since angles $ABE$ and $AEB$ are equal (both are subtended by chord $AB$ at point $E$), triangle $AEB$ is indeed isosceles: $$ \angle ABE = \angle AEB $$
Triangle $AEB$ is isosceles.
More Information
In this triangle, the equal angles indicate that the sides opposite to them are also equal in length. This property of isosceles triangles is fundamental in understanding the relationships in geometry, especially with chord properties in circles.
Tips
- Misidentifying the relationship between angles and failing to apply the Alternate Interior Angles Theorem. To avoid this mistake, clearly label corresponding angles and ensure the lines are parallel before making conclusions about angles.
AI-generated content may contain errors. Please verify critical information