Evaluate the integral ∫ dx / (x^2 √(x^2 + 9))
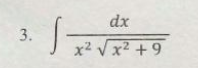
Understand the Problem
The question is asking for the evaluation of the integral, which involves a rational function where the variable x is in both the numerator and the denominator. This requires the application of integration techniques.
Answer
$$ \frac{1}{6} \tan^{-1}\left(\frac{x}{3}\right) + C $$
Answer for screen readers
The final answer is:
$$ \frac{1}{6} \tan^{-1}\left(\frac{x}{3}\right) + C $$
Steps to Solve
- Identify a Suitable Substitution
We will use the substitution ( x = 3 \tan(\theta) ). Therefore, ( dx = 3 \sec^2(\theta) d\theta ). This gives us ( \sqrt{x^2 + 9} = \sqrt{(3 \tan(\theta))^2 + 9} = 3 \sec(\theta) ).
- Substitute into the Integral
Plugging in the substitution into the integral:
$$ \int \frac{dx}{x^2 \sqrt{x^2 + 9}} = \int \frac{3 \sec^2(\theta) d\theta}{(3 \tan(\theta))^2 \cdot 3 \sec(\theta)} $$
This simplifies to:
$$ \int \frac{3 \sec^2(\theta) d\theta}{9 \tan^2(\theta) \cdot 3 \sec(\theta)} = \int \frac{d\theta}{3 \tan^2(\theta)} $$
- Rewrite in Terms of Trigonometric Functions
Using the identity ( \tan^2(\theta) = \sec^2(\theta) - 1 ):
$$ \int \frac{d\theta}{3 (\sec^2(\theta) - 1)} = \frac{1}{3} \int \frac{d\theta}{\sec^2(\theta) - 1} $$
This can further be expressed as:
$$ \int \cos^2(\theta) d\theta $$
- Integrate Using Trigonometric Identity
Now, using the identity:
$$ \cos^2(\theta) = \frac{1 + \cos(2\theta)}{2} $$
Thus, we integrate:
$$ \frac{1}{3} \int \left(\frac{1 + \cos(2\theta)}{2}\right) d\theta = \frac{1}{6} \theta + \frac{1}{6} \sin(2\theta) + C $$
- Back Substitute to Original Variable
Recall that ( \theta = \tan^{-1}\left(\frac{x}{3}\right) ). Hence, substituting back we get:
$$ \frac{1}{6} \tan^{-1}\left(\frac{x}{3}\right) + C $$
The final answer is:
$$ \frac{1}{6} \tan^{-1}\left(\frac{x}{3}\right) + C $$
More Information
The integral represents an application of trigonometric substitution, which is useful for integrals involving square roots of sums of squares. This technique transforms the integral into a more manageable form, ultimately allowing for an explicit solution.
Tips
- Confusing the trigonometric identities. It’s essential to correctly identify ( \sec^2(\theta) ) and use the relationship with ( \tan^2(\theta) ) correctly.
- Forgetting to convert back to the original variable at the end of the integration process.
AI-generated content may contain errors. Please verify critical information