Evaluate the expression (2e) (2 - 1 - 2) / 3
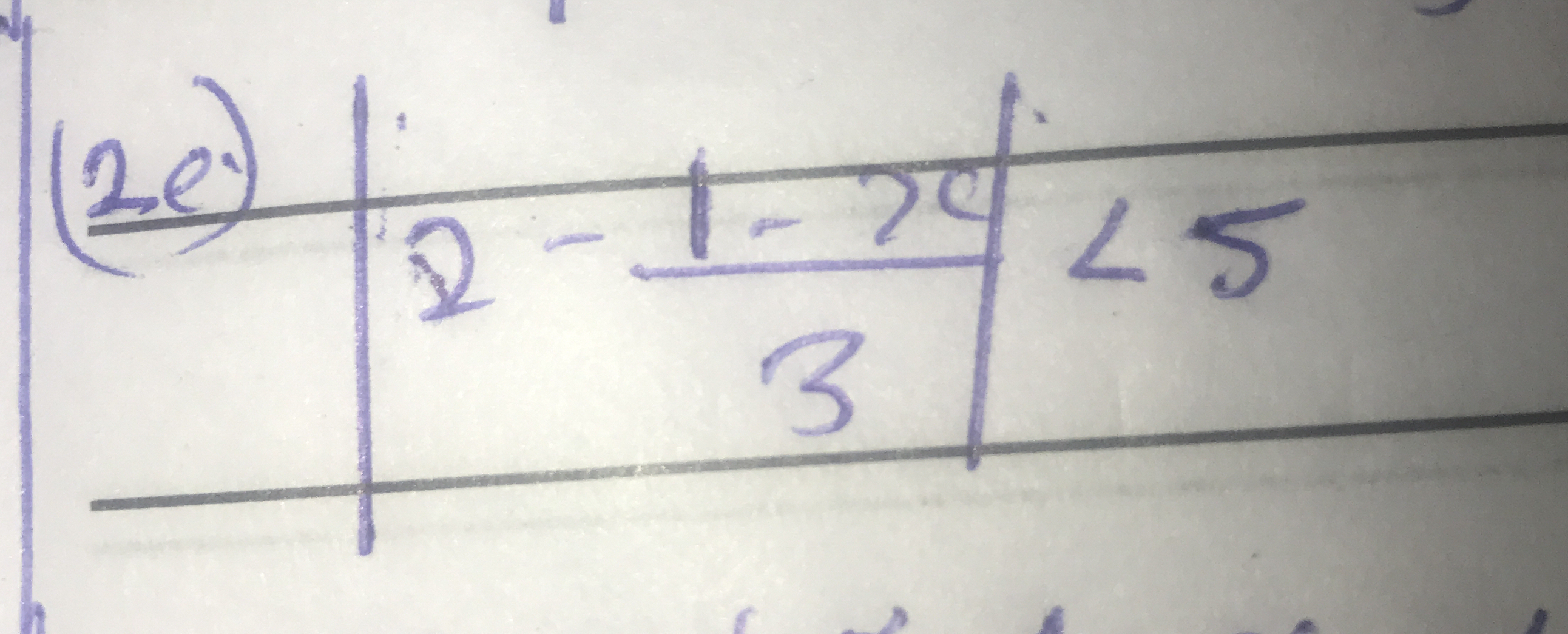
Understand the Problem
The question appears to involve a mathematical expression involving exponents and possibly a calculation, though the specific details are not clear due to the quality of the image. It looks like an equation or calculation needs to be interpreted.
Answer
The result of the expression is $\frac{-2e}{3}$.
Answer for screen readers
The final answer is $\frac{-2e}{3}$.
Steps to Solve
- Identify the components of the expression
The expression is $(2e) \cdot (2 - 1 - 2) / 3$. We need to simplify the expression inside the parentheses first.
- Simplify the expression in parentheses
Calculate $2 - 1 - 2$: $$ 2 - 1 = 1 $$ $$ 1 - 2 = -1 $$ So, the expression becomes $(2e) \cdot (-1) / 3$.
- Multiply the terms
Multiply $(2e)$ by $(-1)$: $$ (2e) \cdot (-1) = -2e $$ Now the expression is $-2e / 3$.
- Final division
Divide by 3: $$ \frac{-2e}{3} $$
The final answer is $\frac{-2e}{3}$.
More Information
In this expression, $e$ is the base of the natural logarithm, approximately equal to 2.71828. This expression may have applications in various mathematical fields involving exponential functions.
Tips
- Forgetting to apply the order of operations (PEMDAS/BODMAS) correctly when simplifying the parenthetical terms.
- Misplacing the negative sign when multiplying by $(-1)$.
AI-generated content may contain errors. Please verify critical information