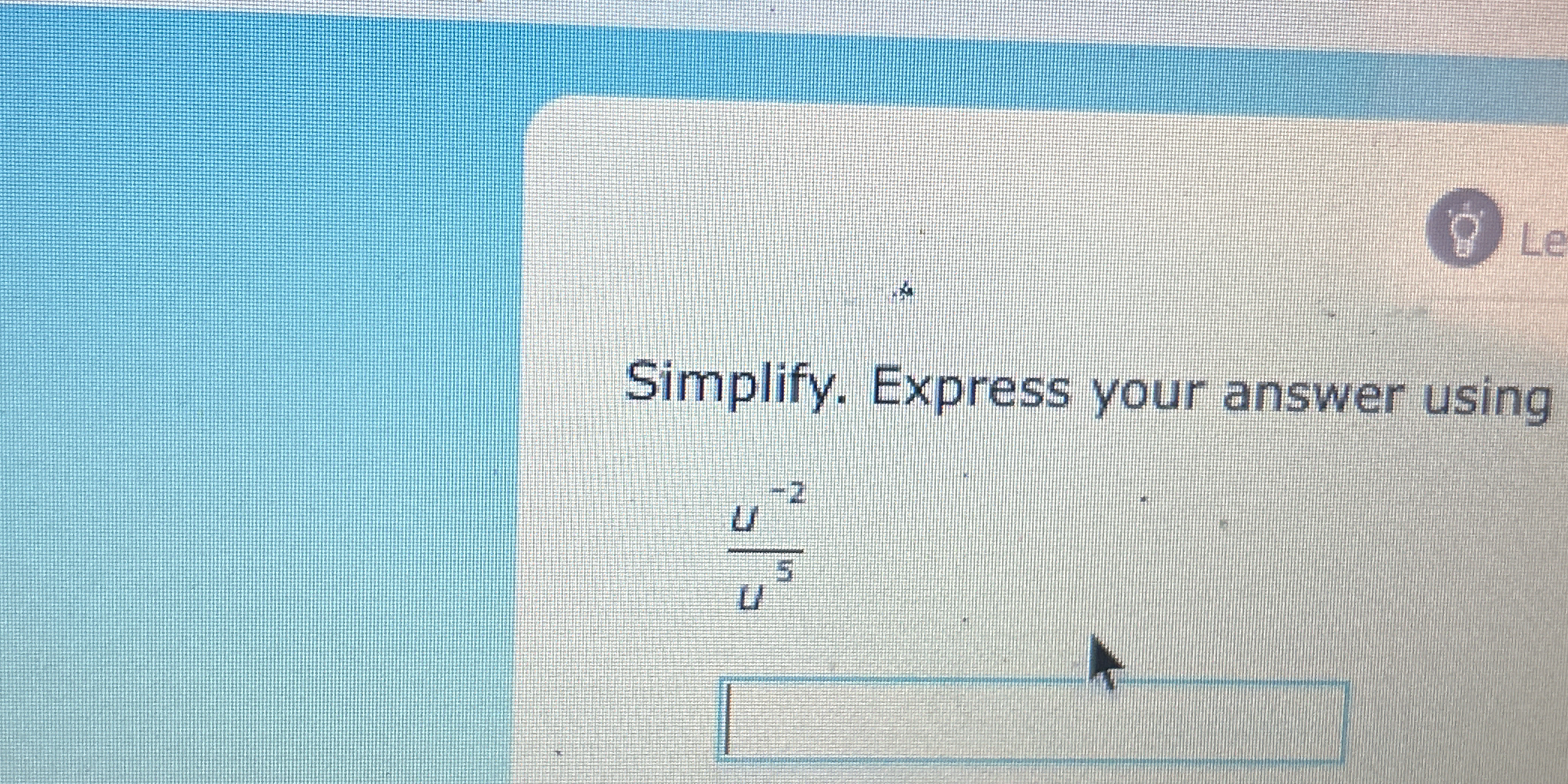
Simplify. Express your answer using u^{-2}/u^{5}.
Understand the Problem
The question is asking to simplify the expression \frac{u^{-2}}{u^{5}} and express the answer using standard notation.
Answer
The simplified answer is $$ \frac{1}{u^{7}} $$
Answer for screen readers
The simplified expression is
$$ \frac{1}{u^{7}} $$
Steps to Solve
- Identify the expression to simplify
The expression we need to simplify is
$$ \frac{u^{-2}}{u^{5}} $$
- Apply the quotient rule for exponents
When dividing powers with the same base, subtract the exponents:
$$ \frac{u^a}{u^b} = u^{a-b} $$
So in this case, we have:
$$ -2 - 5 $$
- Calculate the exponent
Now, calculate the exponent:
$$ -2 - 5 = -7 $$
- Rewrite the expression with the simplified exponent
After calculating the exponent, we can rewrite the expression:
$$ u^{-7} $$
- Convert to standard notation
To express $u^{-7}$ in standard notation (with positive exponents), we use:
$$ u^{-7} = \frac{1}{u^{7}} $$
The simplified expression is
$$ \frac{1}{u^{7}} $$
More Information
The simplification process uses the properties of exponents, specifically the quotient rule, which states how to handle the division of like bases by subtracting their exponents. Expressions with negative exponents can be rewritten as fractions with positive exponents.
Tips
- Forgetting to subtract exponents: Students often mistakenly add the exponents instead of subtracting them when using the quotient rule.
- Leaving negative exponents: Failing to convert negative exponents into a fraction format can sometimes occur.
AI-generated content may contain errors. Please verify critical information