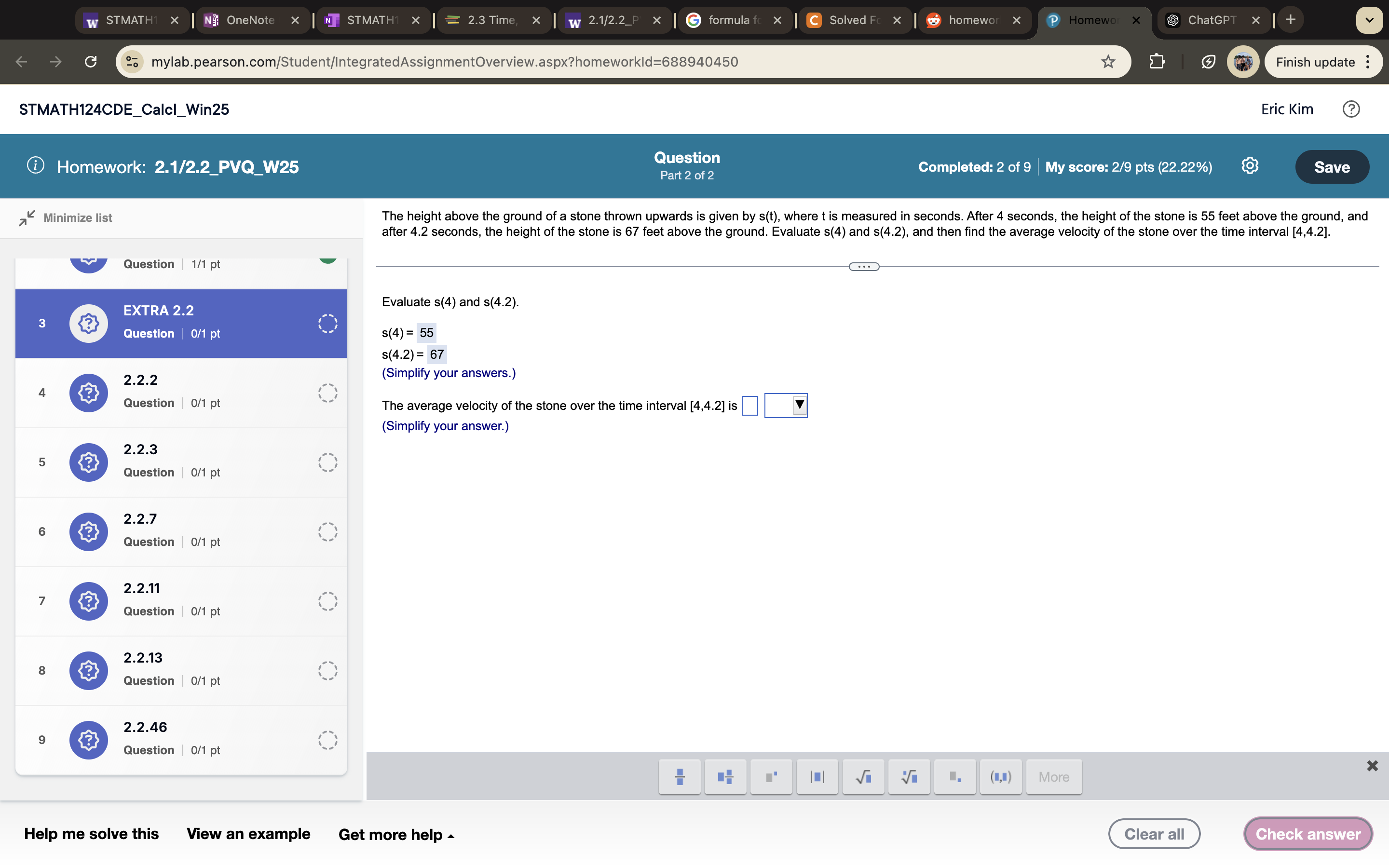
Evaluate s(4) and s(4.2). Then find the average velocity of the stone over the time interval [4, 4.2].
Understand the Problem
The question is asking to evaluate the height of a stone at two specific time points (4 seconds and 4.2 seconds) and then to find the average velocity of the stone over the time interval from 4 to 4.2 seconds.
Answer
The average velocity of the stone over the time interval [4, 4.2] is 60 feet per second.
Answer for screen readers
The average velocity of the stone over the time interval [4, 4.2] is 60 feet per second.
Steps to Solve
-
Evaluate s(4)
Given that at 4 seconds, the height of the stone is already provided as $s(4) = 55$ feet. -
Evaluate s(4.2)
The height of the stone at 4.2 seconds is also given as $s(4.2) = 67$ feet. -
Find the average velocity
To find the average velocity over the interval [4, 4.2], use the formula:
$$\text{Average Velocity} = \frac{s(4.2) - s(4)}{4.2 - 4}$$
Substituting the known values:
$$\text{Average Velocity} = \frac{67 - 55}{4.2 - 4} = \frac{12}{0.2}$$ -
Calculate the average velocity
Simplify the expression:
$$\text{Average Velocity} = \frac{12}{0.2} = 60 \text{ feet per second}$$
The average velocity of the stone over the time interval [4, 4.2] is 60 feet per second.
More Information
The average velocity gives a measure of how fast the stone is moving during the short interval from 4 seconds to 4.2 seconds. This change in height divided by the change in time illustrates the stone's motion.
Tips
- Confusing height values or mistakenly substituting incorrect values for $s(4)$ or $s(4.2)$. Always use specified values directly from the problem.
- Miscalculating the average velocity by not correctly performing the division or subtraction in the formula. Double-check arithmetic.
AI-generated content may contain errors. Please verify critical information