Evaluate lim (x,y)→(1,0) (x - 1)² ln x / ((x - 1)² + y²) and lim (x,y)→(0,0) 2x²y / (x⁴ + y²).
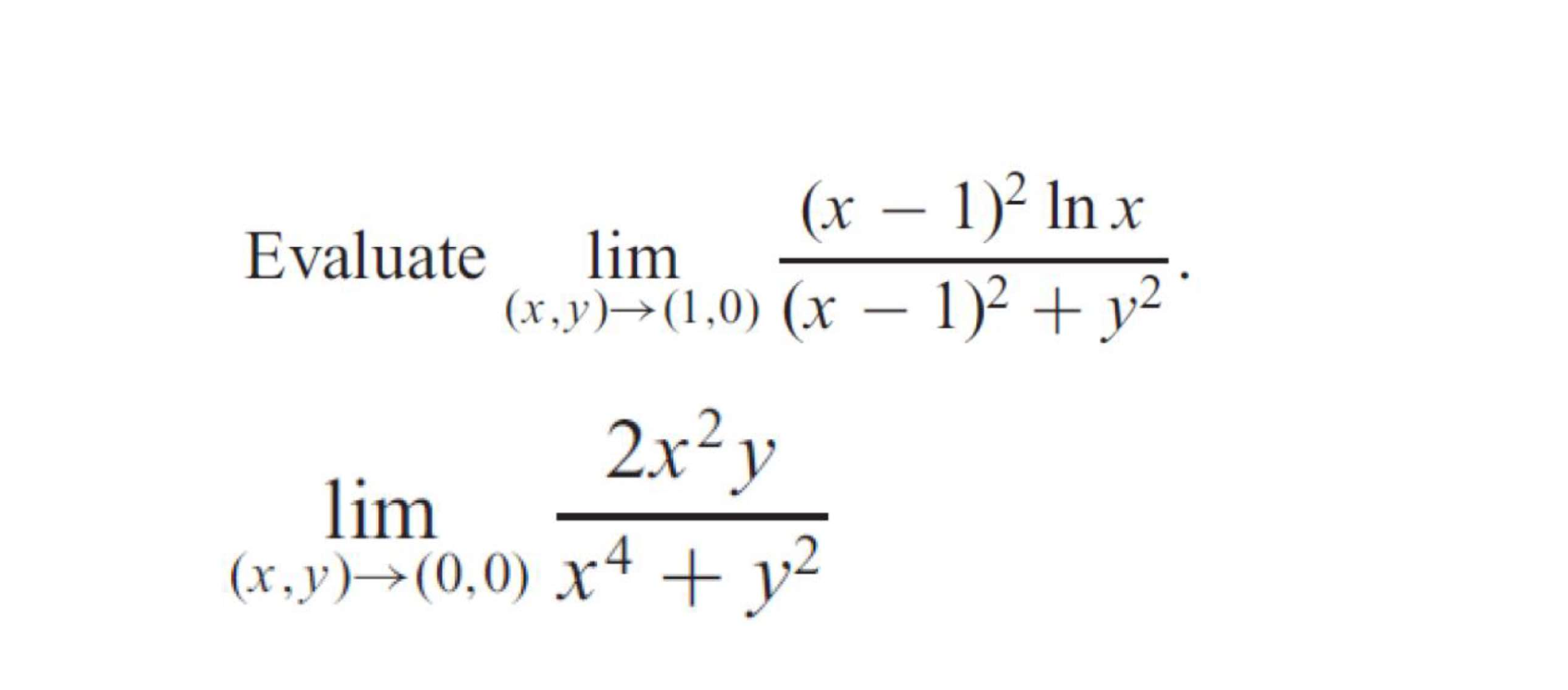
Understand the Problem
The question is asking to evaluate two limits as (x,y) approaches specific points. The first limit involves the function (x - 1)² ln x divided by (x - 1)² + y² as (x,y) approaches (1,0). The second limit involves the expression 2x²y divided by x⁴ + y² as (x,y) approaches (0,0). The problem is to find the calculated values of these limits.
Answer
The limits are \( \frac{1}{2} \) and \( 0 \).
Answer for screen readers
The calculated values of the limits are:
- ( \frac{1}{2} )
- ( 0 )
Steps to Solve
-
Evaluate the first limit
We want to find:
$$ \lim_{(x,y) \to (1,0)} \frac{(x - 1)^2 \ln x}{(x - 1)^2 + y^2} $$
Substituting ( x = 1 ) gives ( (1 - 1)^2 \ln 1 = 0 ), and for ( y = 0 ), we have ( (1 - 1)^2 + 0^2 = 0 ) in the denominator. Thus, we have an indeterminate form ( \frac{0}{0} ). -
Apply L'Hôpital's Rule for the first limit
Since we have an indeterminate form, we can apply L'Hôpital's Rule. Differentiate the numerator and the denominator with respect to ( x ) while treating ( y ) as constant:
- Derivative of the numerator:
$$ \frac{d}{dx}[(x-1)^2 \ln x] = 2(x-1) \ln x + (x-1) $$ - Derivative of the denominator:
$$ \frac{d}{dx}[(x-1)^2 + y^2] = 2(x-1) $$
Thus our limit becomes:
$$ \lim_{(x,y) \to (1,0)} \frac{2(x-1) \ln x + (x-1)}{2(x-1)} $$
-
Simplify and substitute for the first limit
We can simplify:
$$ = \lim_{(x,y) \to (1,0)} \frac{\ln x + 1}{2} $$
Substituting ( x = 1 ):
$$ = \frac{\ln 1 + 1}{2} = \frac{0 + 1}{2} = \frac{1}{2} $$ -
Evaluate the second limit
Next limit to evaluate:
$$ \lim_{(x,y) \to (0,0)} \frac{2x^2 y}{x^4 + y^2} $$
Substituting ( x = 0 ) and ( y = 0 ) gives ( \frac{0}{0} ). -
Convert to polar coordinates for the second limit
In polar coordinates, set ( x = r \cos \theta ) and ( y = r \sin \theta ), and as ( r \to 0 ):
$$ = \lim_{r \to 0} \frac{2(r \cos \theta)^2 (r \sin \theta)}{(r \cos \theta)^4 + (r \sin \theta)^2} $$
This simplifies to:
$$ = \lim_{r \to 0} \frac{2r^3 \cos^2 \theta \sin \theta}{r^4 \cos^4 \theta + r^2 \sin^2 \theta} = \lim_{r \to 0} \frac{2r \cos^2 \theta \sin \theta}{r^2 \cos^4 \theta + \sin^2 \theta} $$ -
Evaluate the limit for the second limit
As ( r \to 0 ), the limit becomes:
$$ = \frac{0}{\sin^2 \theta} = 0 $$
Thus, the final limits are:
- The first limit is ( \frac{1}{2} )
- The second limit is ( 0 )
The calculated values of the limits are:
- ( \frac{1}{2} )
- ( 0 )
More Information
The use of L'Hôpital's Rule is essential for evaluating limits that yield indeterminate forms. In the second limit, converting to polar coordinates simplifies the evaluation, particularly when approaching points like ( (0,0) ).
Tips
- Forgetting to apply L'Hôpital's Rule when encountering indeterminate forms.
- Not substituting or simplifying correctly after differentiation.
- Failing to convert to polar coordinates when dealing with limits approaching ( (0,0) ).