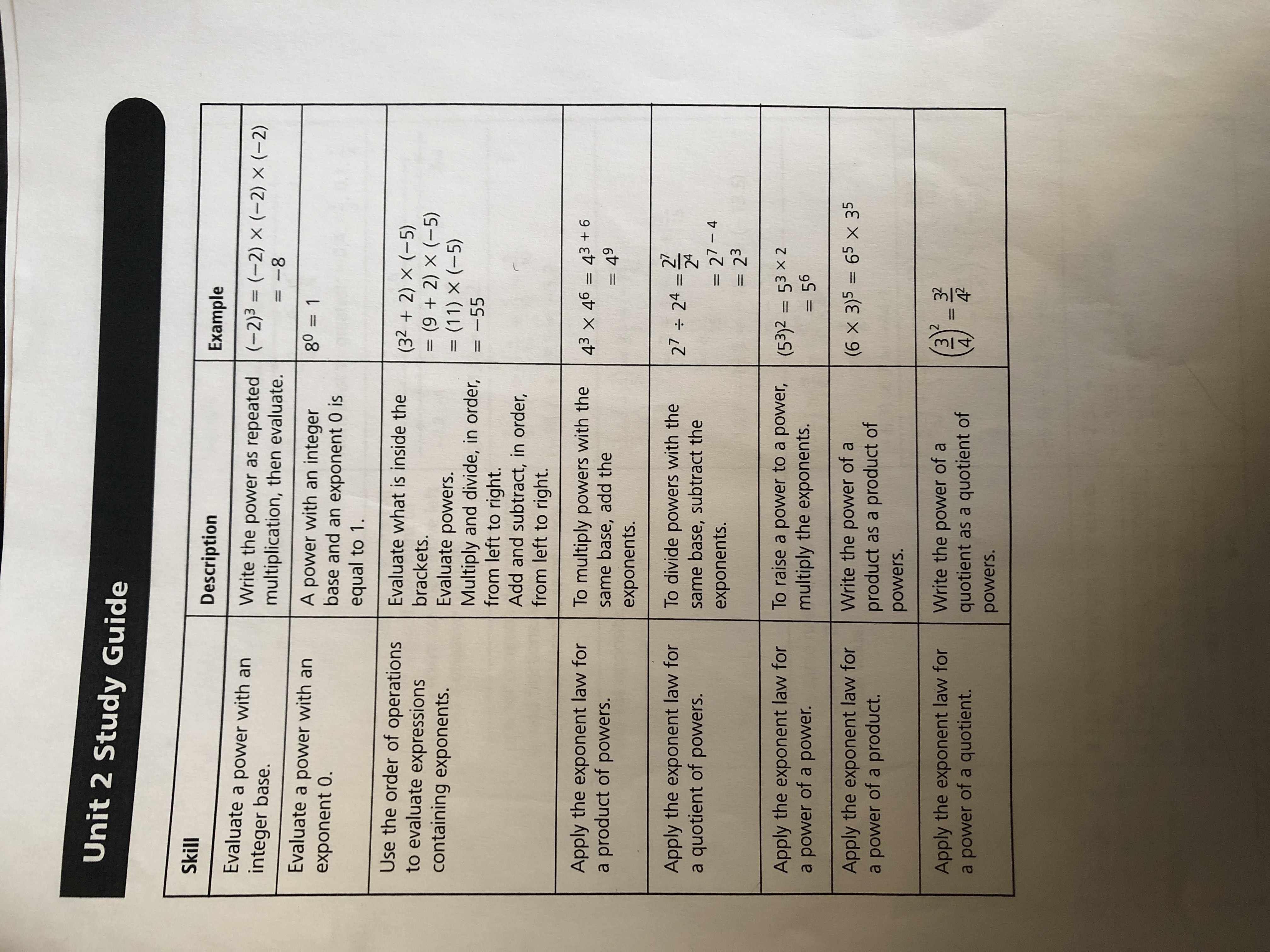
Evaluate a power with an integer base and apply the exponent laws as shown in the provided study guide.

Steps to Solve

1. Evaluate the power with an integer base
   For the power $(-2)^3$, writing it as repeated multiplication gives:
   $$(-2)^3 = (-2) \times (-2) \times (-2)$$

2. Calculate the multiplication
   Now, let's first multiply $(-2) \times (-2)$
   $$(-2) \times (-2) = 4$$
   Next, multiply this result with $(-2)$:
   $$4 \times (-2) = -8$$

3. Confirm complete calculation
   The full calculation shows that $(-2)^3 = -8$.

4. Evaluate with exponent 0
   Next, for $80^0$, we know that any integer base raised to the power of $0$ is $1$:
   $$80^0 = 1$$

5. Use order of operations
   For the example $((32 + 2) \times (-5))$, first, evaluate inside the brackets:
   $$32 + 2 = 34$$
   Now, perform the multiplication:
   $$34 \times (-5) = -170$$

6. Simplifying Powers
   Next, for the power of a product $43 \times 46$, apply the exponent law for a product of powers:
   $$43 \times 46 = 43^{3+6} = 43^9$$

7. Division of Powers
   For instance, applying the exponent law for a quotient of powers, evaluate:
   $$27^7 \div 27^4 = 27^{7-4} = 27^3$$

8. Raising Powers
   To raise a power to a power, using $(5^3)^2$:
   Multiply the exponents:
   $$5^{3 \times 2} = 5^6$$

9. Product of Powers
   For $(6 \times 3)^5$, write it as:
   $$(6)^5 \times (3)^5$$

10. Quotient of Powers
    For $$(\frac{3}{4})^2$$, write it as a quotient of powers:
    $$\frac{3^2}{4^2}$$