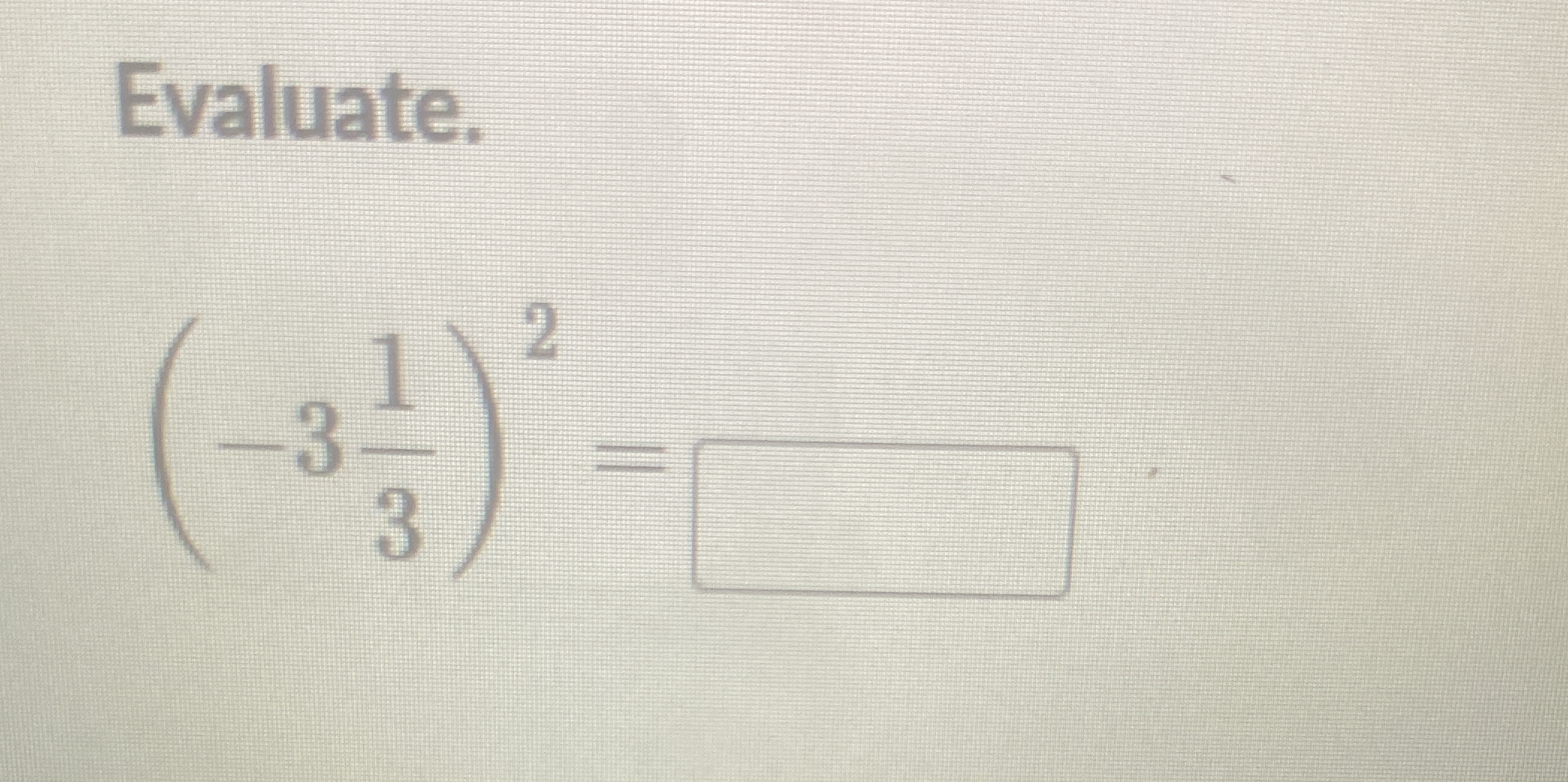
Evaluate. (-3/3)^(1/2)^2 =
Understand the Problem
The question is asking to evaluate the expression (-\frac{3}{3}^{1/2}) raised to the power of 2. This will involve simplifying the expression step-by-step.
Answer
The result of the evaluation is $$ -1 $$
Answer for screen readers
The final answer is
$$ -1 $$
Steps to Solve
- Evaluate the inner expression
Start with the expression inside the parentheses. We have:
$$ -\frac{3}{3} $$
This simplifies to:
$$ -1 $$
- Compute the square root
Now, we take the square root of the simplified expression:
$$ (-1)^{1/2} $$
However, since the square root of a negative number is not defined in the real number system, it results in an imaginary number:
$$ i $$
- Raise to the power of 2
Now, we raise the imaginary result to the power of 2:
$$ (i)^2 $$
Using properties of imaginary numbers, we know that:
$$ (i)^2 = -1 $$
The final answer is
$$ -1 $$
More Information
The expression involves the evaluation of a negative number's square root, which introduces imaginary numbers. It's an interesting reminder of how complex numbers work in math, where the square root of a negative number leads to the imaginary unit (i).
Tips
- One common mistake is assuming that the square root of a negative number is a real number. It's crucial to recognize when to work with imaginary numbers.
- Misplacing the parentheses can also lead to different results, so always double-check the placement of operations.
AI-generated content may contain errors. Please verify critical information