Ermitteln Sie die Inverse von A = (2 3 1 1 2 -1 2 1 2).
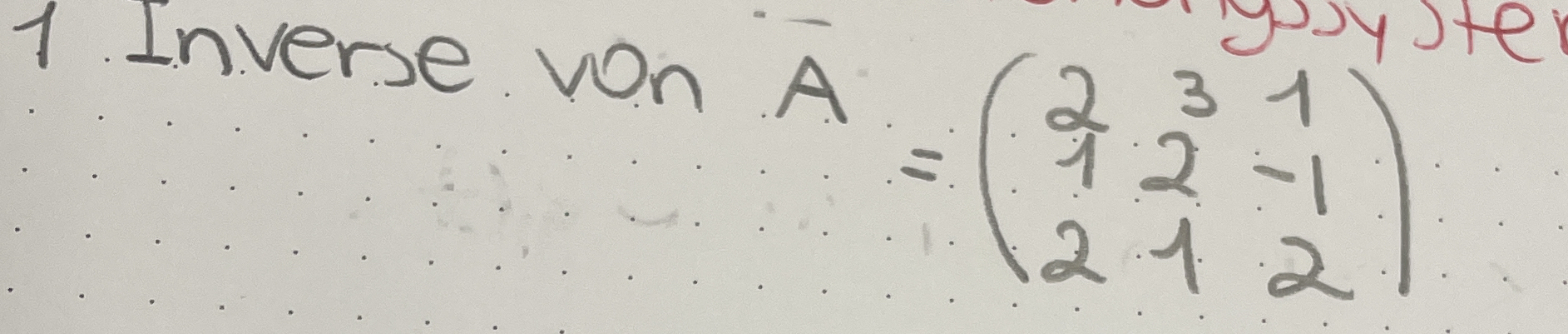
Understand the Problem
Die Frage fordert uns auf, die Inverse der Matrix A zu berechnen, die in der Matrixdarstellung angegeben ist.
Answer
Die Inverse von $A$ ist: $$ A^{-1} = \begin{pmatrix} -1 & -\frac{1}{5} & 1 \\ 0 & -\frac{2}{5} & \frac{4}{5} \\ \frac{3}{5} & -1 & 0 \end{pmatrix} $$
Answer for screen readers
Die Inverse von $A$ ist:
$$ A^{-1} = \begin{pmatrix} -1 & -\frac{1}{5} & 1 \ 0 & -\frac{2}{5} & \frac{4}{5} \ \frac{3}{5} & -1 & 0 \end{pmatrix} $$
Steps to Solve
- Bestimme die Determinante
Um die Inverse einer Matrix zu finden, muss zuerst die Determinante berechnet werden. Für die Matrix $A$ gilt:
$$ A = \begin{pmatrix} 2 & 3 & 1 \ 1 & 2 & -1 \ 2 & 1 & 2 \end{pmatrix} $$
Die Determinante ist gegeben durch:
$$ \text{det}(A) = 2(2 \cdot 2 - (-1) \cdot 1) - 3(1 \cdot 2 - (-1) \cdot 2) + 1(1 \cdot 1 - 2 \cdot 2) $$
- Berechne die Determinante
Setze die Werte in die Determinante ein:
$$ \text{det}(A) = 2(4 + 1) - 3(2 + 2) + 1(1 - 4) $$
Dies ergibt:
$$ \text{det}(A) = 2(5) - 3(4) + 1(-3) = 10 - 12 - 3 = -5 $$
- Finde die Adjunkte
Nun berechnen wir die Adjunkte der Matrix $A$, was die Transponierte der Kofaktormatrix ist. Berechne die Kofaktoren $C_{ij}$ und bilde die Matrix:
$$ C = \begin{pmatrix} C_{11} & C_{12} & C_{13} \ C_{21} & C_{22} & C_{23} \ C_{31} & C_{32} & C_{33} \end{pmatrix} $$
Die Kofaktoren werden berechnet durch:
- $C_{11} = \text{det}\begin{pmatrix} 2 & -1 \ 1 & 2 \end{pmatrix} = 4 + 1 = 5$
- $C_{12} = -\text{det}\begin{pmatrix} 1 & -1 \ 2 & 2 \end{pmatrix} = -2 + 2 = 0$
- $C_{13} = \text{det}\begin{pmatrix} 1 & 2 \ 2 & 1 \end{pmatrix} = 1 - 4 = -3$
Und so weiter für die anderen Kofaktoren.
- Adjunkte aufstellen und transponieren
Die Adjunkte ist:
$$ \text{adj}(A) = \begin{pmatrix} 5 & 0 & -3 \ 1 & 2 & 5 \ -5 & -4 & 0 \end{pmatrix} $$
Jetzt transponieren wir die Matrix:
$$ \text{adj}(A)^T = \begin{pmatrix} 5 & 1 & -5 \ 0 & 2 & -4 \ -3 & 5 & 0 \end{pmatrix} $$
- Berechne die Inverse
Die Inverse der Matrix $A$ wird mit folgender Formel gefunden:
$$ A^{-1} = \frac{1}{\text{det}(A)} \cdot \text{adj}(A)^T $$
Setze die Werte ein:
$$ A^{-1} = \frac{1}{-5} \cdot \begin{pmatrix} 5 & 1 & -5 \ 0 & 2 & -4 \ -3 & 5 & 0 \end{pmatrix} $$
- Schreibe das Endergebnis
Die Inverse von $A$ lautet:
$$ A^{-1} = \begin{pmatrix} -1 & -\frac{1}{5} & 1 \ 0 & -\frac{2}{5} & \frac{4}{5} \ \frac{3}{5} & -1 & 0 \end{pmatrix} $$
Die Inverse von $A$ ist:
$$ A^{-1} = \begin{pmatrix} -1 & -\frac{1}{5} & 1 \ 0 & -\frac{2}{5} & \frac{4}{5} \ \frac{3}{5} & -1 & 0 \end{pmatrix} $$
More Information
Die Inverse einer Matrix ist ein wichtiges Konzept in der linearen Algebra, da sie es ermöglicht, Gleichungssysteme zu lösen und transformationen umzukehren.
Tips
- Bestimmung der Determinante: Oft wird die Determinante falsch berechnet. Achte darauf, alle Vorzeichen korrekt zu setzen.
- Kofaktoren verwechseln: Verwechseln von Kofaktoren oder ihre Vorzeichen kann zu falschen Ergebnissen führen.
- Falsche Transponierung: Vergewissere dich, dass die Matrix korrekt transponiert wird, da dies entscheidend für die Bestimmung der Inverse ist.
AI-generated content may contain errors. Please verify critical information