The trapezoid I'J'K'L' is a dilation of the trapezoid IJKL. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction,... The trapezoid I'J'K'L' is a dilation of the trapezoid IJKL. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction, or a whole number.
Understand the Problem
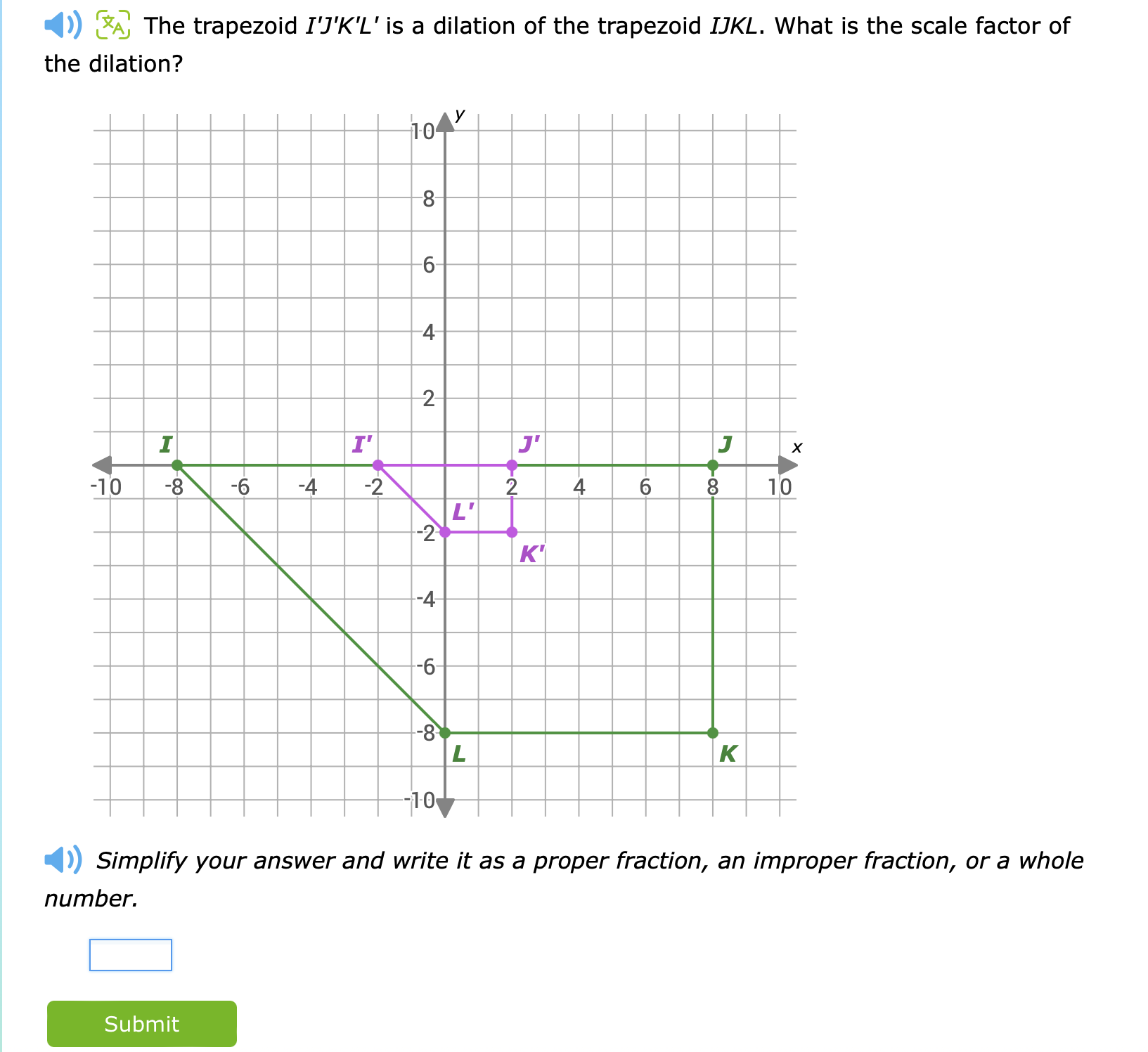
The question is asking for the scale factor of the dilation between two trapezoids, I'J'K'L' and IJKL, using the coordinates provided in the graph. The scale factor is calculated by determining the ratio of corresponding lengths between the two trapezoids.
Answer
The scale factor of the dilation is $\frac{2}{5}$.
Answer for screen readers
The scale factor of the dilation is $\frac{2}{5}$.
Steps to Solve
-
Identify Coordinates of Trapezoids
From the graph, determine the coordinates of the vertices for trapezoids IJKL and I'J'K'L':
- For trapezoid IJKL:
- ( I(-8, -8) )
- ( J(2, -8) )
- ( K(6, -2) )
- ( L(-6, -2) )
- For trapezoid I'J'K'L':
- ( I'(-2, 2) )
- ( J'(2, 2) )
- ( K'(2, -2) )
- ( L'(-2, -2) )
- For trapezoid IJKL:
-
Calculate Lengths of the Bases
Find the lengths of the bases for both trapezoids:
- Length of base ( IJ ): $$ |x_J - x_I| = |2 - (-8)| = 10 $$
- Length of base ( I'J' ): $$ |x_{J'} - x_{I'}| = |2 - (-2)| = 4 $$
-
Determine the Scale Factor
Calculate the scale factor by taking the ratio of the lengths of corresponding bases: $$ \text{Scale Factor} = \frac{\text{Length of base } I'J'}{\text{Length of base } IJ} = \frac{4}{10} $$ $$ = \frac{2}{5} $$
The scale factor of the dilation is $\frac{2}{5}$.
More Information
The scale factor indicates how much the size of trapezoid I'J'K'L' is reduced compared to trapezoid IJKL. A scale factor of $\frac{2}{5}$ means that the dimensions of I'J'K'L' are 40% of the dimensions of IJKL.
Tips
- Forgetting to calculate both corresponding base lengths.
- Incorrectly matching up the corresponding vertices.
- Miscalculating the lengths or the ratio.
AI-generated content may contain errors. Please verify critical information