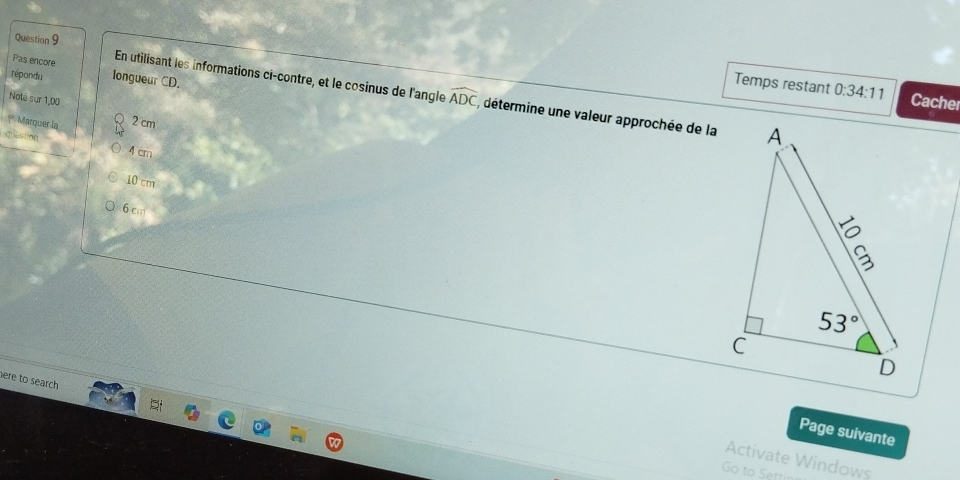
En utilisant les informations ci-contre, et le cosinus de l'angle ADC, déterminez une valeur approchée de la longueur CD.

Steps to Solve

1. Identifiez les données du triangle

On sait que dans le triangle ADC, la longueur du segment AD est de 10 cm, l'angle ADC est de 53°, et la longueur du segment AC est de 2 cm.

2. Appliquez le théorème du cosinus

Le théorème du cosinus est donné par la formule:

$$ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) $$

où $C$ est l'angle entre les côtés $a$ et $b$, et $c$ est le côté opposé à l'angle $C$.

3. Identifiez les valeurs

Ici, nous avons:

• $a = AC = 2 , cm$
• $b = AD = 10 , cm$
• $C = 53^\circ$

Nous voulons trouver la longueur $CD$ qui est le côté opposé à l'angle $C$. Donc, appliquons le théorème:

$$ CD^2 = AC^2 + AD^2 - 2 \cdot AC \cdot AD \cdot \cos(53^\circ) $$

4. Calculez chaque terme

Calculez d'abord $AC^2 = 2^2 = 4$, puis $AD^2 = 10^2 = 100$. Ensuite, calculez le troisième terme:

$$ 2 \cdot AC \cdot AD \cdot \cos(53^\circ) = 2 \cdot 2 \cdot 10 \cdot \cos(53^\circ) $$

Utilisez une calculatrice pour trouver $\cos(53^\circ)$.

5. Effectuez le calcul final

Substituez les valeurs dans l'équation:

$$ CD^2 = 4 + 100 - 40 \cdot \cos(53^\circ) $$

Calculez $CD^2$ et ensuite prenez la racine carrée pour trouver $CD$.