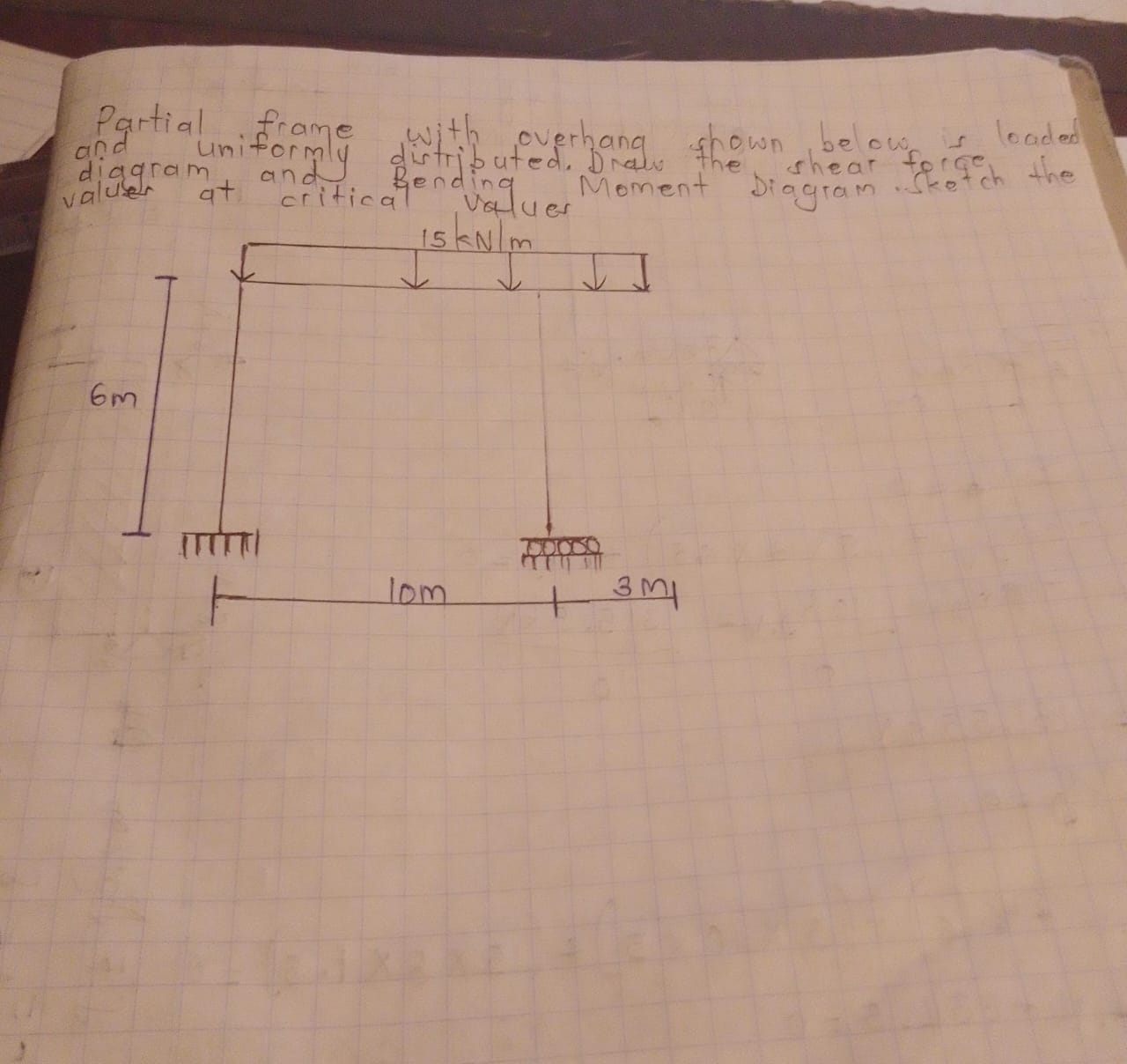
Draw the shear force diagram and bending moment diagram for the given frame loaded with a uniformly distributed load of 15 kN/m and specify the critical values.

Steps to Solve

1. Calculate the total load The total load on the beam due to the uniformly distributed load (UDL) can be calculated using the formula:

   $$ W = w \times L $$

   where ( w = 15 , \text{kN/m} ) and ( L = 10 , \text{m} ).

   Thus,

   $$ W = 15 \times 10 = 150 , \text{kN} $$

2. Determine support reactions Assuming the left end is a fixed support (A) and the right end is a roller support (B), use equilibrium equations to find the reactions. The sum of vertical forces yields:

   $$ R_A + R_B - W = 0 $$

   The moment about point A (taking counter-clockwise moments as positive):

   $$ R_B \times 10 - 150 \times 5 = 0 $$

   From this, solve for ( R_B ):

   $$ R_B = \frac{150 \times 5}{10} = 75 , \text{kN} $$

   Substitute ( R_B ) back into the vertical force equation:

   $$ R_A + 75 - 150 = 0 $$

   Thus,

   $$ R_A = 75 , \text{kN} $$

3. Draw the Shear Force Diagram (SFD) Start from the left (A) and move right:

• From A to the first load:

  • SFD starts at ( +R_A = +75 , \text{kN} )
  • Decrease linearly by $15 , \text{kN/m}$ over $10,m$, resulting in:

  $$ V = 75 - 15x $$

And plot for each segment.

4. Draw the Bending Moment Diagram (BMD) Calculate the moments at various points:

• At A:

  $$ M_A = 0 $$

• At the load:

  • Using the formula for the moment:

  $$ M = R_A \cdot x - w \cdot \frac{x^2}{2} $$

  To find moments at critical locations (A, center of loads, B, etc.), substitute ( x ) to find respective moments.

5. Summarize critical values Identify significant values (max shear and moment) from the SFD and BMD for clarity. Common peaks will occur under the loads and at the supports.