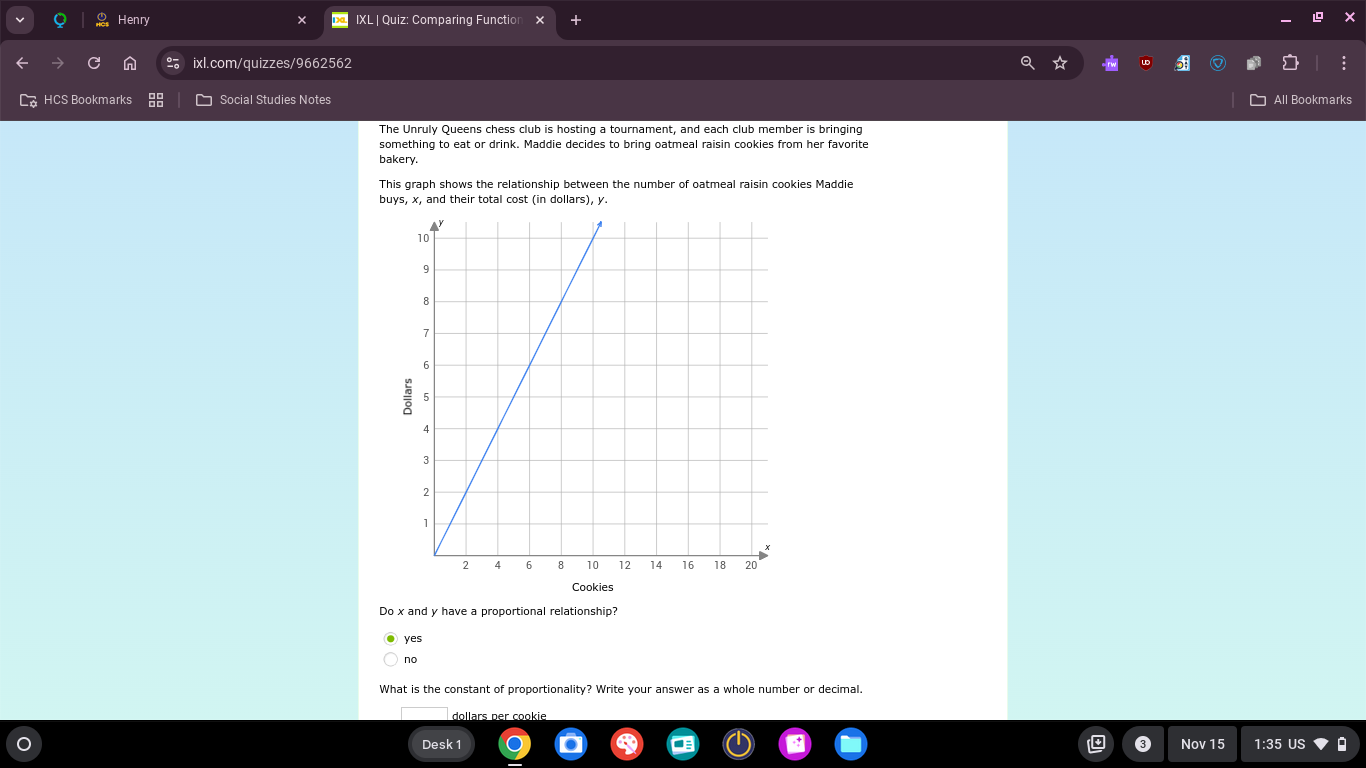
Do x and y have a proportional relationship? What is the constant of proportionality? Write your answer as a whole number or decimal.
Understand the Problem
The question is asking whether the relationship between the number of cookies bought and their total cost is proportional, and it also requests the constant of proportionality, which is the cost per cookie.
Answer
Yes, $2 per cookie.
Answer for screen readers
Yes, the relationship is proportional, and the constant of proportionality is $2 per cookie.
Steps to Solve
- Identify the relationship using the graph
Look at the graph provided. If it shows a straight line passing through the origin (0,0), then the relationship between the number of cookies bought (x-axis) and the total cost (y-axis) is proportional.
- Check for the constant of proportionality
To find the constant of proportionality, we need to determine the slope of the line. The slope can be calculated using two points on the line. For example, take the points (2, 4) and (4, 8).
- Calculate the slope
The formula for slope (m) is given by:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Using our points (2, 4) and (4, 8):
$$ m = \frac{8 - 4}{4 - 2} = \frac{4}{2} = 2 $$
This means that the cost per cookie, or the constant of proportionality, is $2.
Yes, the relationship is proportional, and the constant of proportionality is $2 per cookie.
More Information
Since the graph is a straight line through the origin, it indicates a proportional relationship. The constant of proportionality represents the cost for each cookie purchased.
Tips
- Misidentifying the line's behavior as non-linear when it is straight.
- Failing to calculate the slope accurately. Always ensure to subtract in the correct order.
AI-generated content may contain errors. Please verify critical information