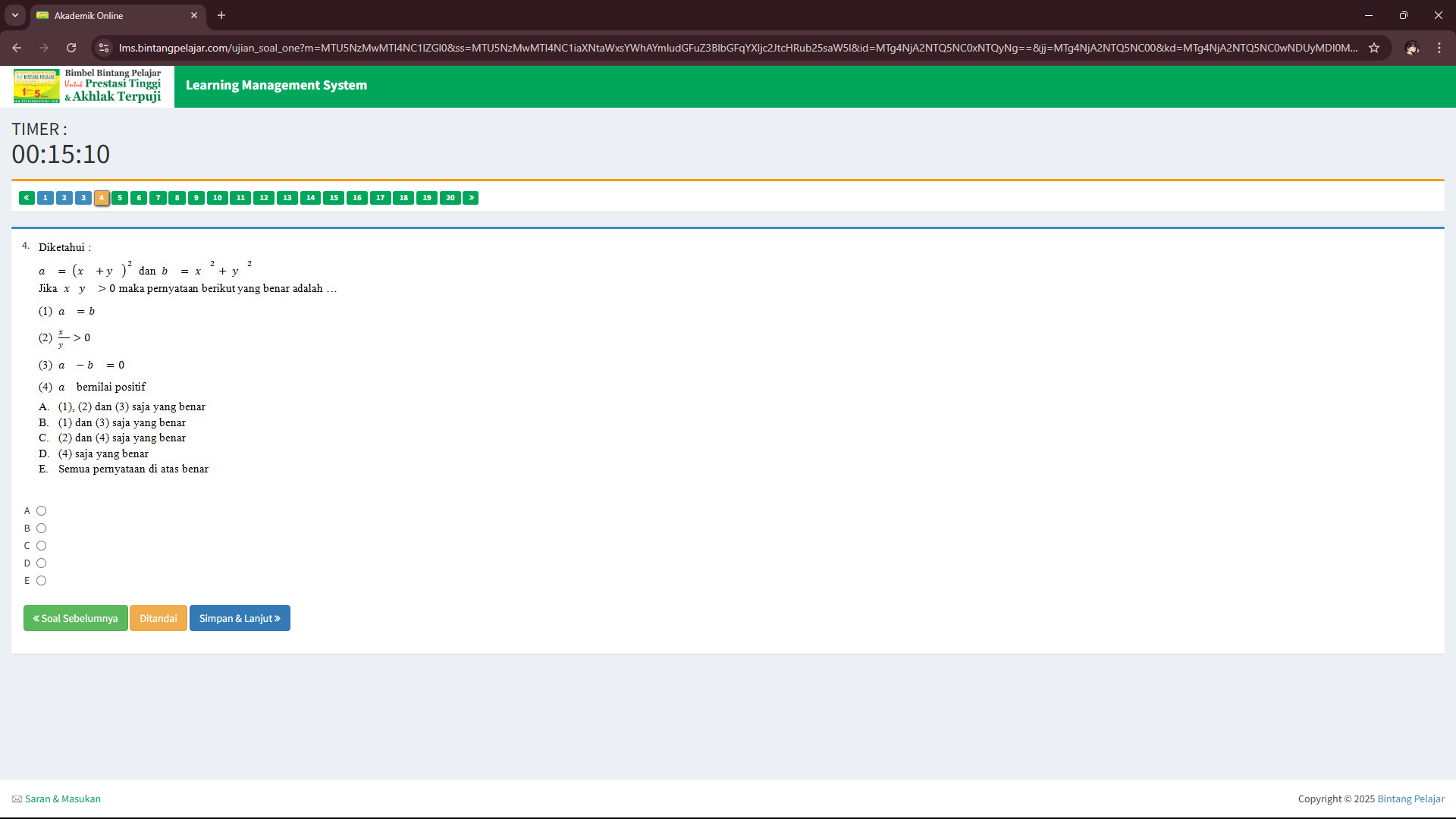
Diketahui: a = (x + y)^2 dan b = x^2 + y^2. Jika x > y > 0 maka pernyataan berikut yang benar adalah ...
Understand the Problem
Pertanyaan ini meminta kita untuk menganalisis persamaan yang diberikan dan memilih pernyataan mana yang benar berdasarkan syarat yang diberikan. Kita harus menentukan kebenaran pernyataan 1, 2, dan 3 mengenai nilai a dan b.
Answer
C. (2) dan (4) saja yang benar
Answer for screen readers
Jawaban yang benar adalah:
C. (2) dan (4) saja yang benar
Steps to Solve
-
Menetapkan Persamaan
Dari soal, kita diberikan:
$$ a = (x + y)^2 $$
$$ b = x^2 + y^2 $$
Selanjutnya, kita perlu mengevaluasi hubungan antara $a$ dan $b$ berdasarkan kondisi $x \neq y$. -
Membandingkan a dan b
Kita ekspansi $a$:
$$(x + y)^2 = x^2 + 2xy + y^2$$
Sehingga,
$$ a = x^2 + 2xy + y^2 $$
Sedangkan $b$ adalah:
$$ b = x^2 + y^2 $$
Dari sini, kita bisa melihat bahwa:
$$ a = b + 2xy $$ -
Menganalisis Kondisi x dan y
Karena $x \neq y$, maka $2xy > 0$ jika $x$ dan $y$ memiliki tanda yang sama (baik positif atau negatif).
Sehingga,
$$ a > b $$
dan
$$ a - b = 2xy > 0 $$ -
Menguji Pernyataan
-
Pernyataan (1): $a = b$
Tidak benar, karena $a > b$. -
Pernyataan (2): $2xy > 0$
Benar, karena $x$ dan $y$ tidak sama dan memiliki tanda yang sama. -
Pernyataan (3): $a - b = 0$
Tidak benar, karena $a - b > 0$. -
Pernyataan (4): $a$ bernilai positif
Benar, karena $a = x^2 + 2xy + y^2$ yang pasti positif jika $x$ dan $y$ tidak sama dan bukan nol.
Dari analisis di atas, hanya pernyataan (2) dan (4) yang benar.
Jawaban yang benar adalah:
C. (2) dan (4) saja yang benar
More Information
Pernyataan yang dievaluasi dalam soal merupakan analisis dari fungsi kuadrat. Kondisi $x \neq y$ menghasilkan bahwa produk $xy$ positif bila keduanya memiliki tanda yang sama, sehingga kesimpulan yang ditarik tentang nilai $a$ dan perbandingannya dengan $b$ dapat diandalkan.
Tips
- Menganggap $a = b$ tanpa melakukan perhitungan ekspansi yang diperlukan.
- Salah memahami pengaruh dari kondisi $x \neq y$, sehingga berpotensi menghasilkan kesimpulan yang tidak tepat.
AI-generated content may contain errors. Please verify critical information