Determine whether the work done by the fisherman, normal force, gravitational force, and frictional force on the sled is positive, negative, or zero.
Understand the Problem
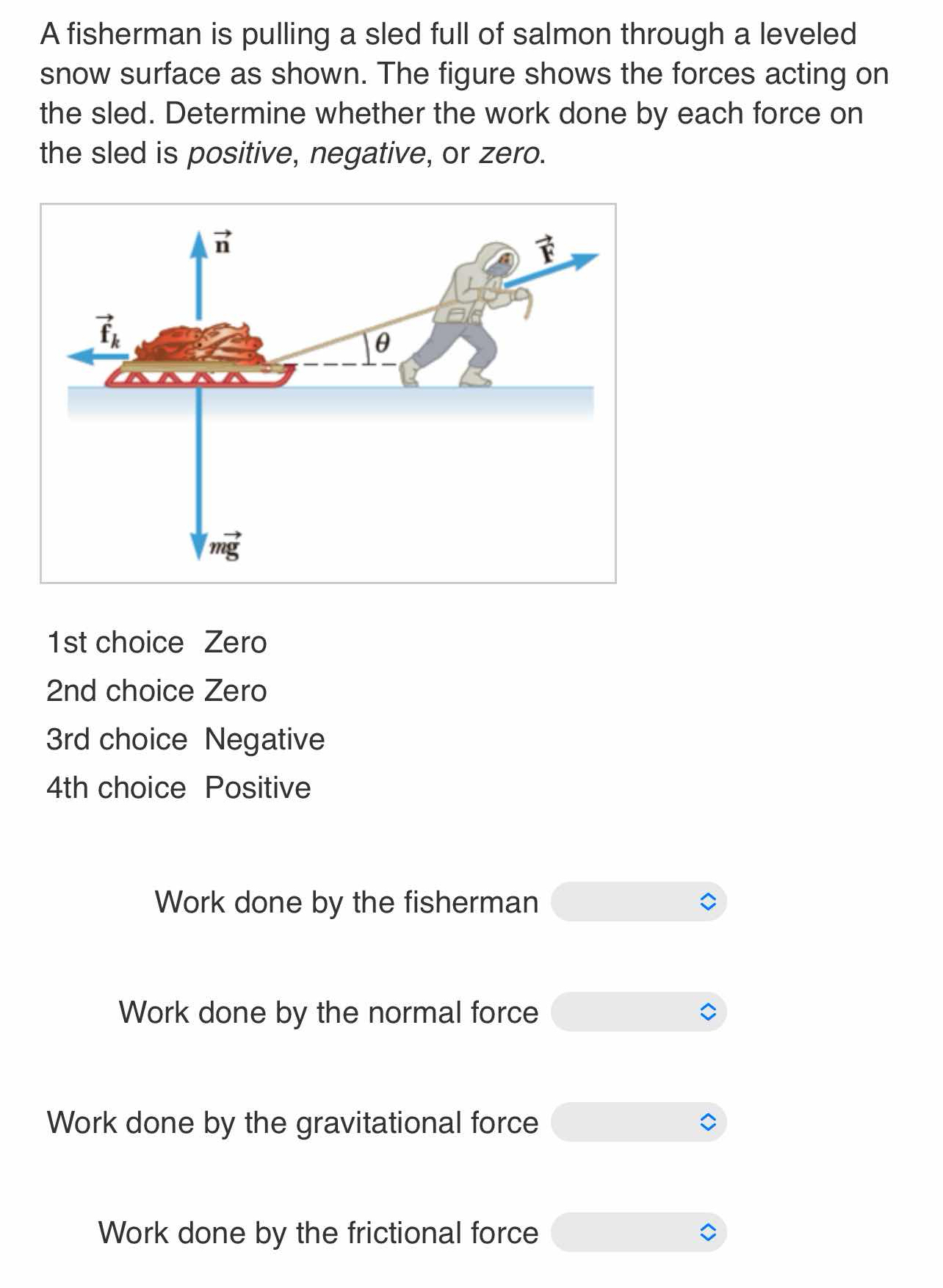
The question is asking to analyze the forces acting on a sled being pulled by a fisherman and determine whether the work done by each force (the fisherman, normal force, gravitational force, and frictional force) is positive, negative, or zero.
Answer
- Work done by fisherman: Positive, Work done by normal force: Zero, Work done by gravitational force: Zero, Work done by frictional force: Negative.
Answer for screen readers
- Work done by the fisherman: Positive
- Work done by the normal force: Zero
- Work done by the gravitational force: Zero
- Work done by the frictional force: Negative
Steps to Solve
-
Identify the forces acting on the sled
The forces acting on the sled include:
- The force applied by the fisherman ($F_f$)
- The gravitational force ($F_g = mg$)
- The normal force ($F_n$)
- The frictional force ($F_k$)
-
Determine the direction of each force
- The force exerted by the fisherman is directed at an angle $\theta$ with respect to the horizontal.
- The gravitational force acts vertically downwards.
- The normal force acts vertically upwards.
- The frictional force acts horizontally opposite to the direction of motion.
-
Analyze work done by the fisherman
Work is calculated as $W = F \cdot d \cdot \cos(\phi)$, where $\phi$ is the angle between the force and the direction of motion. In this case, the fisherman’s force has a component in the direction of motion, so:
- For the fisherman, the work done is positive since the force’s horizontal component and the displacement are in the same direction.
-
Analyze work done by the normal force
The normal force acts perpendicular to the displacement of the sled. Since the angle between the normal force and the displacement is 90 degrees:
- The work done by the normal force is zero ($W_n = F_n \cdot d \cdot \cos(90^\circ) = 0$).
-
Analyze work done by the gravitational force
The gravitational force also acts perpendicular to the direction of displacement on the horizontal surface:
- Thus, the work done by the gravitational force is also zero ($W_g = F_g \cdot d \cdot \cos(90^\circ) = 0$).
-
Analyze work done by the frictional force
The frictional force acts opposite to the direction of motion. Therefore:
- The work done by the frictional force is negative since it opposes the displacement ($W_k = F_k \cdot d \cdot \cos(180^\circ)$).
- Work done by the fisherman: Positive
- Work done by the normal force: Zero
- Work done by the gravitational force: Zero
- Work done by the frictional force: Negative
More Information
- Work is defined as the energy transferred when a force is applied over a distance. The sign of the work indicates whether the force adds energy to the system (positive), removes energy (negative), or does nothing (zero).
- Understanding the angle between forces and displacement is key in determining the sign of the work done.
Tips
- A common mistake is misinterpreting the angle for forces acting vertically when the movement is horizontal, leading to incorrect calculations.
- Confusing normal force with directional vectors; remember that if the force is perpendicular to displacement, the work done is zero.
AI-generated content may contain errors. Please verify critical information