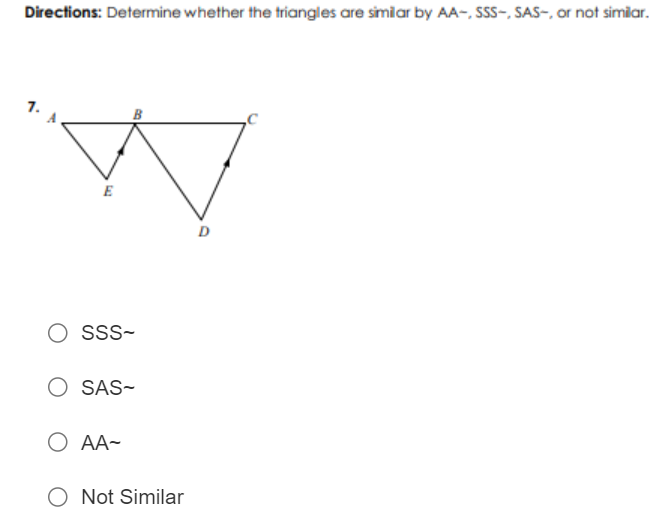
Determine whether the triangles are similar by AA~, SSS~, SAS~, or not similar.
Understand the Problem
The question is asking to determine whether two given triangles are similar based on the similarity criteria of triangles: AA (Angle-Angle), SSS (Side-Side-Side), and SAS (Side-Angle-Side). The user must analyze the diagram and choose the appropriate similarity condition or state if they are not similar.
Answer
The triangles are similar by AA.
Answer for screen readers
The triangles are similar by the AA (Angle-Angle) criterion.
Steps to Solve
-
Identify the Angles Observe the given triangles. Identify the corresponding angles. In this case, the angles at vertices A and C are the same because they are formed by the same transversal. Thus, $\angle A = \angle C$.
-
Identify the Sides Next, check the ratio of the lengths of the sides that correspond to the angles. The sides can be labeled as follows:
- Side opposite to angle A: $AB$ (for triangle ABC)
- Side opposite to angle C: $CD$ (for triangle EDC)
-
Check for Similarity Criteria Using the AA similarity criterion, which states that if two angles of one triangle are equal to two angles of another triangle, the triangles are similar. Since we have identified one pair of equal angles ($\angle A = \angle C$), we can say that the triangles are similar by angle-angle (AA).
-
Confirm with the Second Angle To confirm, we can check the second angles $\angle B$ and $\angle D$. Since the sum of angles in a triangle is 180 degrees, if one angle is equal, the other two must also equal, thus confirming similarity.
The triangles are similar by the AA (Angle-Angle) criterion.
More Information
Triangles are similar when they have the same shape, which can be proved using different similarity criteria such as AA, SSS, and SAS. In this case, AA was sufficient to determine similarity.
Tips
- Misidentifying angles or assuming three pairs of sides need to be checked for AA similarity. Only two angles are required.
- Forgetting to check corresponding sides or angles might lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information