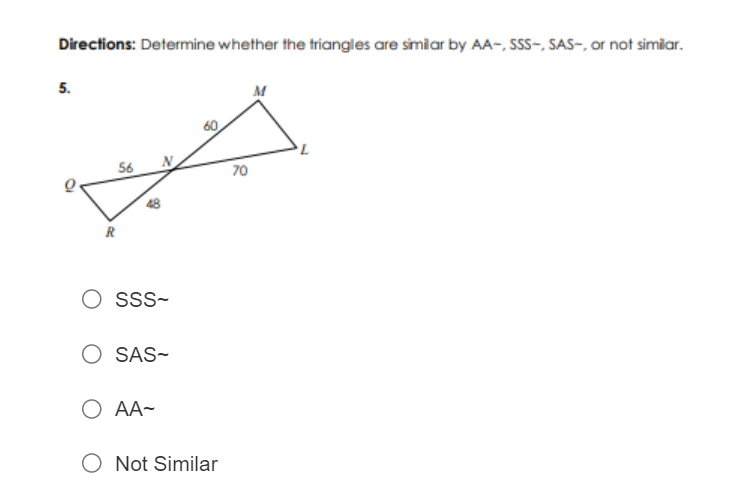
Determine whether the triangles are similar by AA~, SSS~, SAS~, or not similar.

Steps to Solve

1. Identify Angles and Sides of Both Triangles

From the image, identify the angles and side lengths of the triangles. For triangle ( RQ ):

• Angle ( R = 56^\circ )
• Side ( RQ = 48 )

For triangle ( NML ):

• Angle ( N = ? ) (We need to find this)
• Side ( NL = 60 )

2. Use Triangle Angle Sum Theorem

The sum of the angles in a triangle is ( 180^\circ ).

For triangle ( RQ ):

• Let angle ( Q = x ).
• Then angle ( P = 180^\circ - (56^\circ + x) ).

For triangle ( NML ), using the side opposite to the angles:

• The corresponding angle ( L ) can be calculated based on the given angles and the needed side measurements.

3. Calculate Corresponding Angles

Since ( Q ) is not given, we can use the rule that states that if two angles are known, we can conclude the third angle. Assuming that angle ( L ) corresponds with angle ( R ):

• If ( L = 70^\circ ), then angle ( N = 180^\circ - (L + M) = 180^\circ - 70^\circ - x ).

4. Calculate Ratios of Sides (SSS Criterion)

Now we will see if the sides are proportional:

• Ratios of corresponding sides: $$ \frac{RQ}{NL} = \frac{48}{60} = 0.8 $$

Next, you check if the remaining side ( QM ) (not given but can be derived if necessary) and compare with the respective side in the triangle ( NML ).

5. Determine Similarity Criteria

• If the angles are equal (AA), or if the ratios of the corresponding sides are equal (SSS), or if two sides are proportional with the included angle being equal (SAS).

Using these determined angles and side lengths, identify the matching criteria which would give you the classification.