Determine the value of λ and μ so that the equations 2x + 3y + 5z = 9, 7x + 3y - 2z = 8, 2x + 3y + λz = μ have (i) no solution, (ii) a unique solution, and (iii) infinite many solu... Determine the value of λ and μ so that the equations 2x + 3y + 5z = 9, 7x + 3y - 2z = 8, 2x + 3y + λz = μ have (i) no solution, (ii) a unique solution, and (iii) infinite many solutions.
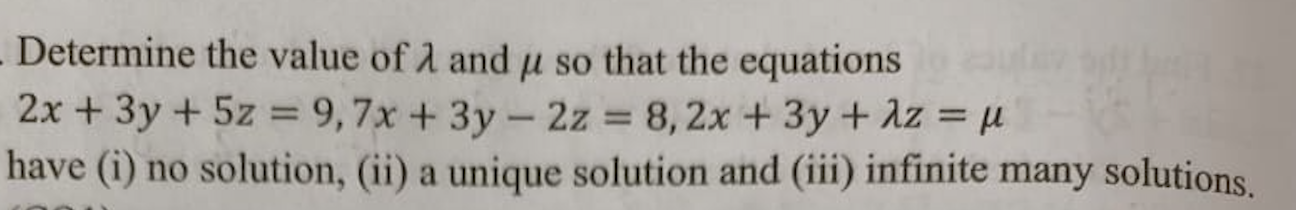
Understand the Problem
The question is asking to find the values of λ and μ such that the given system of equations will produce three different cases of solutions: no solution, a unique solution, and infinitely many solutions. This typically involves analyzing the conditions for the determinant of the coefficient matrix and the consistency of the equations.
Answer
- No solution: $\lambda = 6$ (inconsistent $\mu$) - Unique solution: $\lambda \neq 6$ - Infinite solutions: $\lambda = 6$, $\mu = 9$
Answer for screen readers
- No solution: $\lambda = 6$ (with an inconsistent $ \mu$)
- Unique solution: $\lambda \neq 6$
- Infinite solutions: $\lambda = 6$, $\mu = 9$
Steps to Solve
- Set up the augmented matrix
The given system of equations can be represented in augmented matrix form. The equations are:
- $2x + 3y + 5z = 9$
- $7x + 3y - 2z = 8$
- $2x + 3y + \lambda z = \mu$
The augmented matrix is:
$$ \begin{bmatrix} 2 & 3 & 5 & | & 9 \ 7 & 3 & -2 & | & 8 \ 2 & 3 & \lambda & | & \mu \end{bmatrix} $$
- Find the determinant for unique solutions
For the system to have a unique solution, the determinant of the coefficient matrix must not be zero. The coefficient matrix is:
$$ A = \begin{bmatrix} 2 & 3 & 5 \ 7 & 3 & -2 \ 2 & 3 & \lambda \end{bmatrix} $$
The determinant can be calculated using:
$$ \text{det}(A) = 2(3\lambda + 6) - 3(7\lambda - 10) + 5(21 - 6) $$
Set this determinant not equal to zero for a unique solution.
- Conditions for no solution
For the system to have no solution, the determinant must be zero, and the system must be inconsistent. This occurs when the third equation is inconsistent with the first two when the determinant is zero.
To enforce a no-solution condition, set the determinant to zero and check if the system of equations still holds for valid $(\lambda, \mu)$ pairs: $$ \text{det}(A) = 0 $$
- Conditions for infinite solutions
For the system to have infinitely many solutions, the determinant must also be zero, but the equations must be consistent. This usually means one equation can be written as a linear combination of the others. So, we need to set $\lambda$ and $\mu$ in such a way that:
-
The determinant is zero.
-
The last row can be expressed as a combination of the first two rows.
-
Solve the determinant expression
Calculate the determinant expression:
$$ \text{det}(A) = 6 - 3 \lambda + 3 \lambda - 21 = -3(\lambda - 6) $$
- For unique solution: $-3(\lambda - 6) \neq 0 \Rightarrow \lambda \neq 6$.
- For no solution: Set $\lambda = 6$.
- For infinite solutions: When $\lambda = 6$, also set $\mu = 9$ (this ensures consistency).
- No solution: $\lambda = 6$ (with an inconsistent $ \mu$)
- Unique solution: $\lambda \neq 6$
- Infinite solutions: $\lambda = 6$, $\mu = 9$
More Information
In systems of linear equations, unique, no, or infinite solutions depend on the relationships among the equations, often expressed through the determinant of the coefficient matrix. These conditions assess if the equations intersect at a single point, are parallel (no solution), or are collinear (infinitely many solutions).
Tips
- Incorrectly interpreting when the determinant is zero or non-zero.
- Forgetting to assess the consistency of equations when $\lambda$ or $\mu$ is set.
- Not applying the elimination method correctly to verify conditions.
