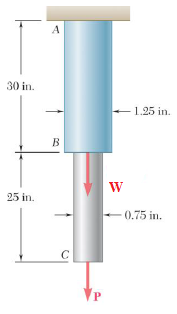
Determine the relationship between the pressure P and weight W in the given system based on the dimensions provided.
Understand the Problem
The question is asking us to analyze the forces acting on a system involving a pipe and determine how pressure P relates to the weight W based on the dimensions provided. To solve this, we will need to apply fluid mechanics principles and possibly equations relating pressure, area, and weight.
Answer
$$ W = P \cdot A_C $$
Answer for screen readers
The relationship between the pressure (P) and the weight (W) can be expressed as:
$$ W = P \cdot A_C $$
Where (A_C) is the area of the cross-section of the lower cylinder.
Steps to Solve
- Identify the system configuration
The problem involves two cylindrical sections: the upper cylinder with diameter (d_A = 1.25 , \text{in}) and height (h_A = 30 , \text{in}), and the lower cylinder with diameter (d_C = 0.75 , \text{in}) and height (h_C = 25 , \text{in}).
- Calculate the areas of the cross-sections
Use the formula for the area of a circle, (A = \pi \left(\frac{d}{2}\right)^2) for both cross-sections:
- For the upper cylinder (A):
$$ A_A = \pi \left(\frac{1.25}{2}\right)^2 = \pi \left(0.625\right)^2 = \pi (0.390625) $$
- For the lower cylinder (C):
$$ A_C = \pi \left(\frac{0.75}{2}\right)^2 = \pi \left(0.375\right)^2 = \pi (0.140625) $$
- Determine the weight W of the fluid in the upper cylinder
The weight (W) is equal to the volume of fluid times the density. The volume (V_A) of the fluid in the upper cylinder can be calculated using:
$$ V_A = A_A \cdot h_A $$
Thus, the weight is:
$$ W = V_A \cdot \rho g $$
Where (\rho g) is the weight density of the fluid.
- Relate the pressure P to the weight W and area A_C
The pressure exerted by the weight at the base of the lower cylinder can be defined as:
$$ P = \frac{W}{A_C} $$
Thus, substituting for (W):
$$ P = \frac{V_A \cdot \rho g}{A_C} $$
- Express the relationship between P and W
Rearranging the equation gives us:
$$ W = P \cdot A_C $$
This shows how pressure (P) relates to the weight (W).
The relationship between the pressure (P) and the weight (W) can be expressed as:
$$ W = P \cdot A_C $$
Where (A_C) is the area of the cross-section of the lower cylinder.
More Information
The analysis reveals that pressure acting on a surface is equal to the weight of the fluid above it divided by the area of that surface. This principle is fundamental in fluid mechanics, highlighting the relationship between pressure and weight within fluid systems.
Tips
- Confusing the areas of the sections; always ensure you use the correct diameter for each section.
- Neglecting to convert units if necessary; make sure all dimensions are consistent before calculations.
AI-generated content may contain errors. Please verify critical information