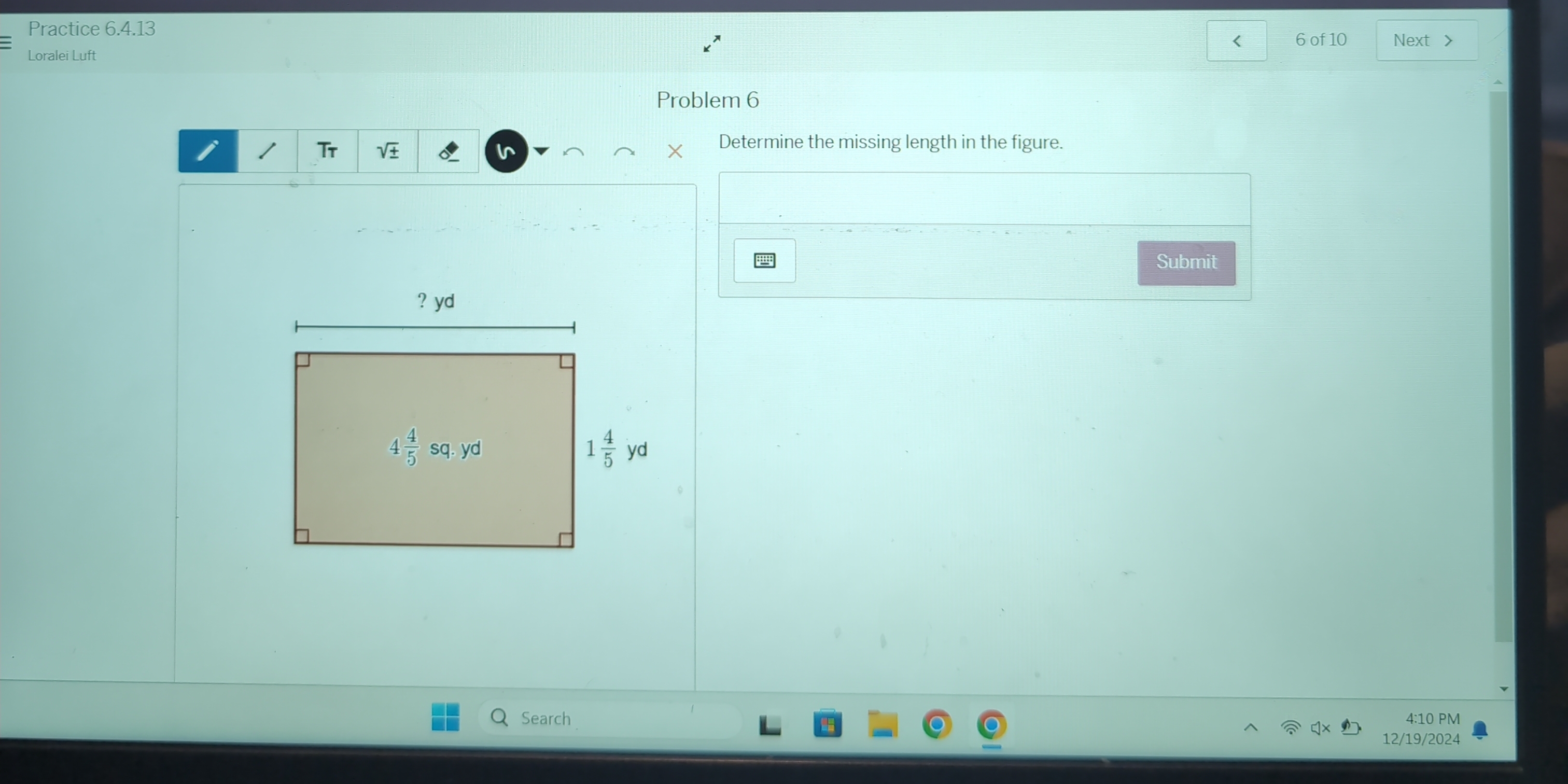
Determine the missing length in the figure.

Steps to Solve

1. Identify the known values

The area of the rectangle is given as $4 \frac{4}{5}$ square yards, and one of the dimensions is $1 \frac{1}{4}$ yards.

2. Convert the mixed numbers to improper fractions

To simplify calculations, convert $4 \frac{4}{5}$ and $1 \frac{1}{4}$ to improper fractions:

For $4 \frac{4}{5}$: $$ 4 \frac{4}{5} = \frac{4 \times 5 + 4}{5} = \frac{20 + 4}{5} = \frac{24}{5} $$

For $1 \frac{1}{4}$: $$ 1 \frac{1}{4} = \frac{1 \times 4 + 1}{4} = \frac{4 + 1}{4} = \frac{5}{4} $$

3. Apply the area formula of a rectangle

The area of a rectangle is given by the formula: $$ \text{Area} = \text{Length} \times \text{Width} $$

We need to find the missing side, which we’ll denote as $x$. Thus, we can set up the equation: $$ \frac{24}{5} = x \times \frac{5}{4} $$

4. Solve for the missing dimension

To isolate $x$, divide both sides by $\frac{5}{4}$: $$ x = \frac{24}{5} \div \frac{5}{4} $$

This can be rewritten as: $$ x = \frac{24}{5} \times \frac{4}{5} $$

5. Perform the multiplication

Multiply the fractions: $$ x = \frac{24 \times 4}{5 \times 5} = \frac{96}{25} $$

6. Convert back to a mixed number if needed

To convert $\frac{96}{25}$ to a mixed number: $$ 96 \div 25 = 3 \text{ remainder } 21 $$

So, we have: $$ \frac{96}{25} = 3 \frac{21}{25} $$