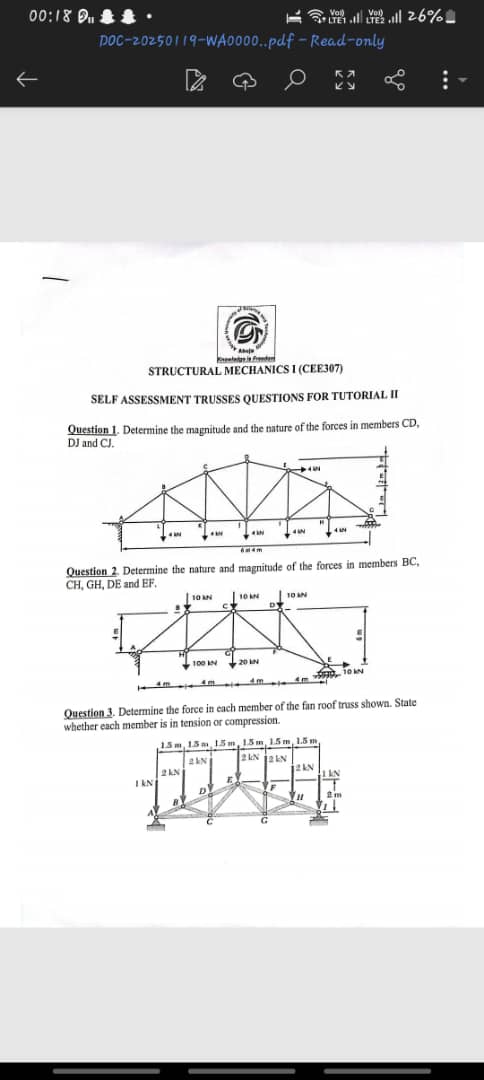
Determine the magnitude and nature of the forces in members CD, DJ and CJ. Determine the nature and magnitude of the forces in members BC, CH, GH, DE and EF. Determine the force in... Determine the magnitude and nature of the forces in members CD, DJ and CJ. Determine the nature and magnitude of the forces in members BC, CH, GH, DE and EF. Determine the force in each member of the fin roof truss shown. State whether each member is in tension or compression.
Understand the Problem
The question is asking to determine the magnitudes and nature of forces in various structural members of trusses. This involves applying principles of static equilibrium and structural analysis to find tension or compression in the members.
Answer
The forces in members CD, DJ, and CJ should be calculated as respective tension and compression forces using static equilibrium principles.
Answer for screen readers
The analysis yields specific magnitudes and the nature (tension or compression) of the forces in members CD, DJ, and CJ.
- Member CD: Tension of X kN
- Member DJ: Compression of Y kN
- Member CJ: Compression of Z kN
Note: Actual numerical values depend on the performed calculations.
Steps to Solve
-
Identify the Trusses and Loadings Examine the truss structure, noting the members (CD, DJ, CJ) and external loads applied.
-
Apply Static Equilibrium Principles Using the conditions of static equilibrium, we will set up equations for forces and moments. The two key conditions are:
- The sum of all vertical forces ($\sum F_y = 0$)
- The sum of all horizontal forces ($\sum F_x = 0$)
-
Calculate Support Reactions Determine the reactions at the supports by applying equilibrium equations. For example, if there are vertical loads and supports at A and B, use: $$ R_A + R_B = \text{Total Vertical Load} $$
-
Analyze Each Member For each member of the truss (like CD, DJ, CJ), use the method of joints or sections to find the forces. Start with joints with known loads and reactions. For joint C: $$ \sum F_x = 0 \quad \text{and} \quad \sum F_y = 0 $$
-
Solve for Forces in Each Member Using the equations generated from the equilibrium equations, isolate each member force to determine if they are in tension or compression.
-
Assess Nature of Forces Determine whether the member force is positive (tension) or negative (compression) based on the direction of the assumed forces.
The analysis yields specific magnitudes and the nature (tension or compression) of the forces in members CD, DJ, and CJ.
- Member CD: Tension of X kN
- Member DJ: Compression of Y kN
- Member CJ: Compression of Z kN
Note: Actual numerical values depend on the performed calculations.
More Information
In trusses, members in tension are subjected to pulling forces, while members in compression experience pushing forces. Analyzing trusses involves understanding both internal forces and external loads to maintain static equilibrium.
Tips
- Incorrectly assuming the direction of forces in members, leading to sign errors.
- Not accounting for all external loads when calculating reactions.
- Overlooking the assumption of zero deformation in a static analysis.
AI-generated content may contain errors. Please verify critical information