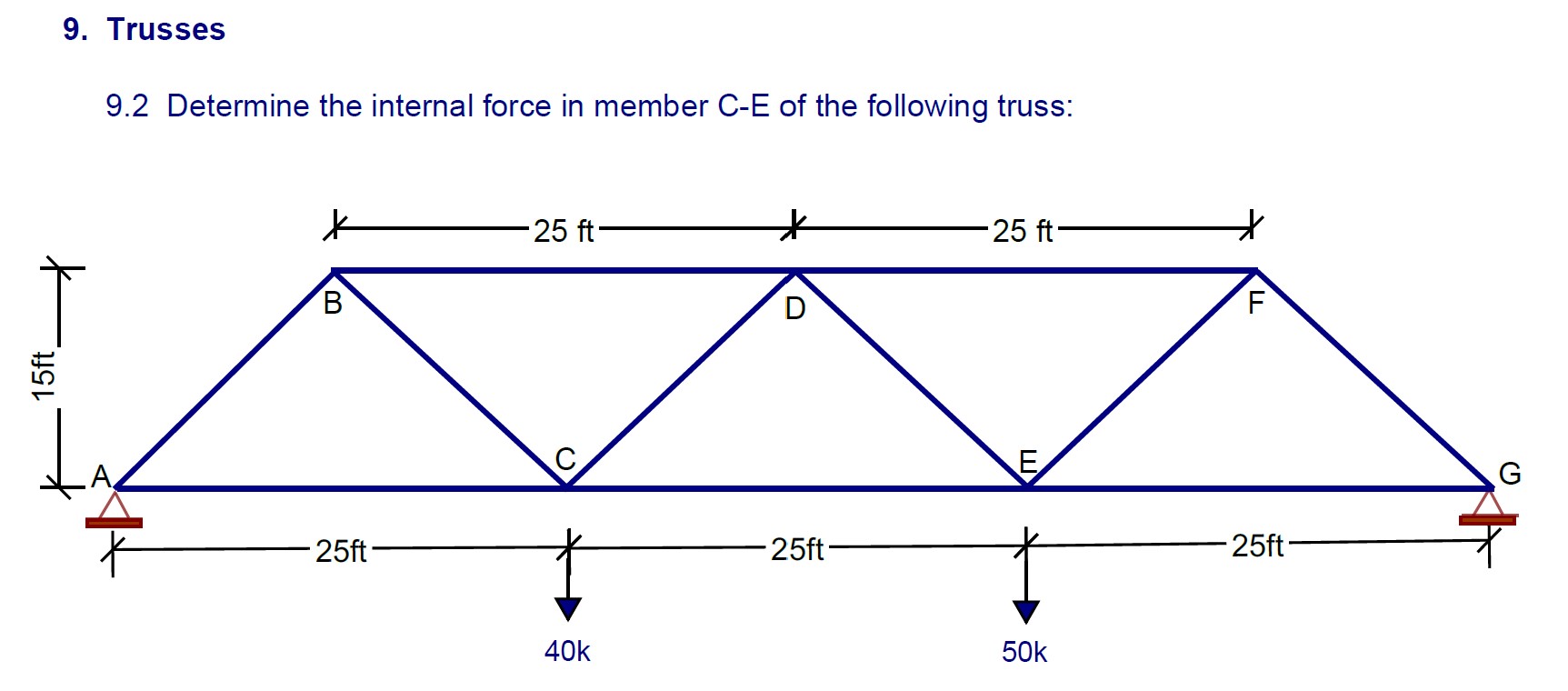
Determine the internal force in member C-E of the following truss.

Steps to Solve

1. Determine Reactions at Supports First, calculate the reactions at the supports (A and G). Use the equations of static equilibrium:

   • Sum of vertical forces ($\sum F_y = 0$)
   • Sum of moments around one support ($\sum M = 0$).

   Given the applied loads of 40 kips and 50 kips, set up the equations.

   $$ R_A + R_G - 40k - 50k = 0 $$

   Now, taking moments about point A:

   $$ -50k \times 75ft + R_G \times 100ft = 0 $$

   From here, solve for $R_G$ and then substitute $R_G$ back into the first equation to find $R_A$.

2. Draw Free Body Diagrams for Members Now, isolate member C-E and draw a free body diagram. Identify all forces acting on members C and E, including axial forces, applied loads, and reactions.

3. Apply Method of Joints Use the method of joints, specifically focusing on joint D where member C-E connects. Write the equilibrium equations:

   • Sum of horizontal forces ($\sum F_x = 0$)
   • Sum of vertical forces ($\sum F_y = 0$).

   For joint D, express forces in terms of tension (or compression) in members C and E.

   $$ F_C + F_E \cos(\theta) = 0 $$ $$ F_E \sin(\theta) - V_D = 0 $$

4. Find the Angle Calculate the angle $\theta$ of member C-E using geometry. Since the height is 15 ft and the base is 25 ft:

   $$ \theta = \tan^{-1}\left(\frac{15}{25}\right) $$

   Use this angle to find the sine and cosine values.

5. Solve for Internal Forces Substitute known values into your force equations to solve for $F_E$ (the internal force in member C-E). Ensure all components are expressed in consistent units.