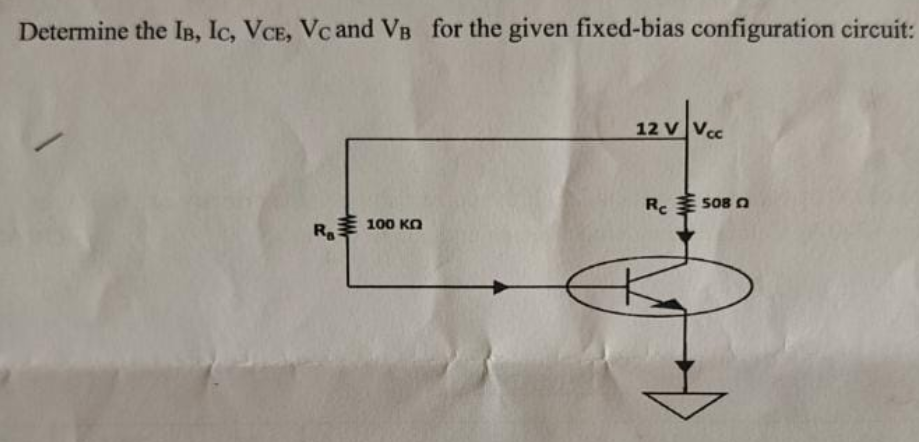
Determine the IB, IC, VCE, VC and VB for the given fixed-bias configuration circuit.

Steps to Solve

1. Find the Base Voltage (VB)

The base voltage ($V_B$) can be calculated using the voltage divider formula. The voltage from the supply ($V_{CC}$) is divided among the resistors $R_B$ and the base-emitter junction of the transistor.

$$ V_B = V_{CC} \cdot \frac{R_B}{R_B + R_E} $$

Where $R_E$ is typically the resistance between the emitter and ground. In this scenario, we will assume it is equal to $0 , \Omega$ for simplicity.

$$ V_B = 12V \cdot \frac{100kΩ}{100kΩ + 0Ω} = 12V $$

2. Calculate Base Current (IB)

Using the base-emitter voltage drop ($V_{BE}$), typically around $0.7V$ for silicon transistors, we can find the base current ($I_B$) with Ohm’s Law:

$$ I_B = \frac{V_B - V_{BE}}{R_B} $$

$$ I_B = \frac{12V - 0.7V}{100kΩ} = \frac{11.3V}{100kΩ} = 0.000113 A = 113 \mu A $$

3. Find Collector Current (IC)

The collector current ($I_C$) can be approximated using the transistor's current gain ($\beta$). Assuming a $\beta$ value of around 100:

$$ I_C \approx \beta \cdot I_B $$

$$ I_C \approx 100 \cdot 113 \mu A = 11.3 mA $$

4. Find Collector-Emitter Voltage (VCE)

Next, we find the collector-emitter voltage ($V_{CE}$) using Kirchhoff’s Voltage Law in the output loop:

$$ V_{CE} = V_{CC} - I_C \cdot R_C $$

Calculating $V_{CE}$:

$$ V_{CE} = 12V - (11.3 mA \cdot 508Ω) $$

Converting the collector current into Amperes:

$$ I_C = 11.3 mA = 0.0113 A $$

Thus,

$$ V_{CE} = 12V - (0.0113 A \cdot 508Ω) = 12V - 5.7404 V \approx 6.2596 V $$

5. Calculate Collector Voltage (VC)

The collector voltage ($V_C$) can then be calculated by:

$$ V_C = V_{CC} - I_C \cdot R_C $$

Using the previous values:

$$ V_C = 12V - 5.7404 V \approx 6.2596 V $$

6. Summary:

To summarize, we have calculated:

• $I_B \approx 113 \mu A$
• $I_C \approx 11.3 mA$
• $V_{CE} \approx 6.2596V$
• $V_C \approx 6.2596V$
• $V_B = 12V$