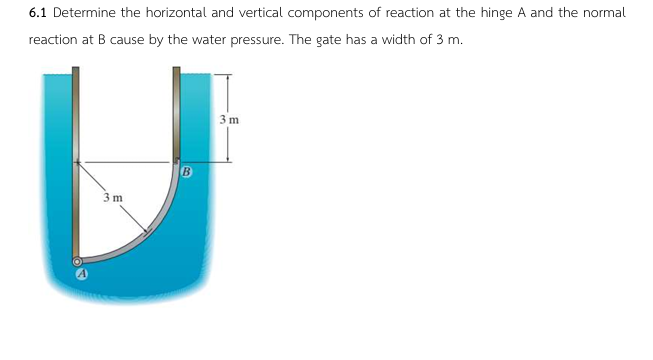
Determine the horizontal and vertical components of reaction at the hinge A and the normal reaction at B caused by the water pressure. The gate has a width of 3 m.

Steps to Solve

1. Calculate the Pressure at Depth The pressure exerted by a fluid in a static condition is given by the equation: $$ P = \rho g h $$ where:

• $P$ is the pressure at depth,
• $\rho$ is the density of water (approximately (1000 , \text{kg/m}^3)),
• $g$ is the acceleration due to gravity ((9.81 , \text{m/s}^2)),
• $h$ is the depth of the water (3 m in this case).

2. Determine the Total Force Exerted by Water on the Gate The total force is calculated by multiplying the pressure by the surface area of the gate: $$ F = P \cdot A $$ The area (A) for the submerged gate (width times height) is: $$ A = \text{width} \times \text{height} = 3 , \text{m} \times 3 , \text{m} = 9 , \text{m}^2 $$

3. Calculate the Reaction Force Due to Water Pressure Using the average pressure across the submerged gate, we first find: $$ P = 1000 \cdot 9.81 \cdot 3 = 29430 , \text{Pa} $$

Now, calculate total force: $$ F = P \cdot A = 29430 \cdot 9 = 264870 , \text{N} $$

4. Find the Location of the Center of Pressure The center of pressure (h_{cp}) for a vertical surface can be determined with the formula: $$ h_{cp} = \frac{I_G}{A \cdot h} + h_{c} $$ where:

• (I_G) is the moment of inertia of the area about its top edge, which for a rectangle is: $$ I_G = \frac{b h^3}{3} = \frac{3 \cdot 3^3}{3} = 27 , \text{m}^4 $$
• (h_c) is the depth at which the pressure is acting, which is halfway up the height: (h_c = \frac{3}{2} = 1.5 , \text{m}).

Calculating: $$ h_{cp} = \frac{27}{9 \cdot 3} + 1.5 = 1 + 1.5 = 2.5 , \text{m} $$

5. Calculate Horizontal and Vertical Components of Reaction at Hinge A Components can be found by considering the equilibrium of forces:

• Vertical Reaction at hinge A, (R_y) counteracts the upward force: $$ R_y + F = 0 \quad \Rightarrow \quad R_y = -F = -264870 , \text{N} $$

• Horizontal Reaction at hinge A, (R_x) must counteract the force acting due to water pressure: Since there’s no other horizontal force, (R_x = F_{h} = F).

6. Determine the Normal Reaction at Point B The normal reaction (N) at point B can be calculated by understanding that it must counteract the vertical forces acting on B and is equal to the vertical reaction at hinge A since it only has vertical components.