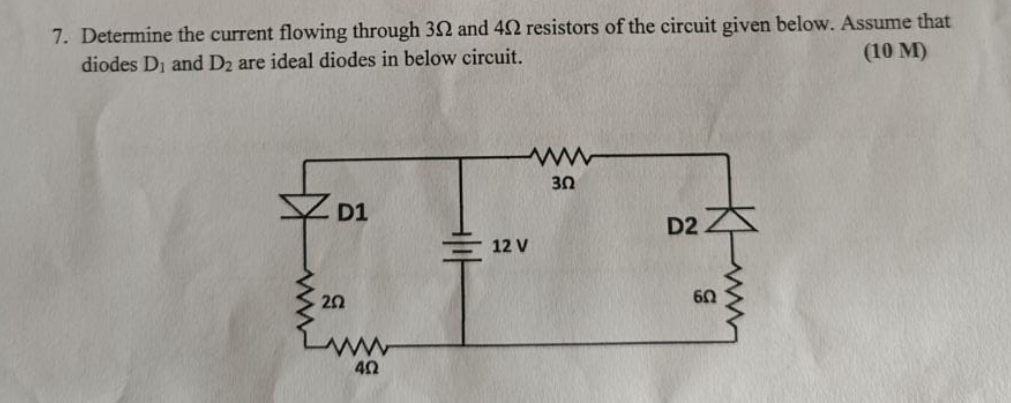
Determine the current flowing through 3Ω and 4Ω resistors of the circuit given below. Assume that diodes D1 and D2 are ideal diodes in below circuit.

Steps to Solve

1. Identify the Circuit Configuration We have resistors and two ideal diodes (D1 and D2). The diodes will only allow current in one direction when they are forward-biased.

2. Determine Diode States For our given circuit with a 12 V supply:

• Diode D1 is forward-biased because it allows current to flow in the direction from the positive side of the battery.
• Diode D2 is also forward-biased due to the same reasoning. Thus, both diodes conduct current.

3. Simplify the Circuit Since both diodes are conducting, the resistors can be analyzed in combination:

• The 2Ω resistor is in series with the 3Ω resistor.
• The 4Ω and 6Ω resistors are in parallel; we can calculate their equivalent resistance.

4. Calculate Equivalent Resistance Calculate the equivalent resistance of the 4Ω and 6Ω resistors in parallel using the formula: $$ R_{eq} = \frac{R_1 \times R_2}{R_1 + R_2} $$ Substituting values: $$ R_{eq} = \frac{4 \times 6}{4 + 6} = \frac{24}{10} = 2.4 , \Omega $$

5. Combine Resistors and Calculate Total Resistance Now, add the resistance of the top series combination (2Ω + 3Ω = 5Ω) to the equivalent resistance: $$ R_{total} = 5 , \Omega + 2.4 , \Omega = 7.4 , \Omega $$

6. Use Ohm's Law to Determine Total Current According to Ohm's Law ($V = IR$), we can find the total current in the circuit: $$ I = \frac{V}{R_{total}} = \frac{12 , V}{7.4 , \Omega} \approx 1.622 , A $$

7. Determine Current Through the Resistors The same current flows through the 3Ω and 2Ω resistors due to their series connection. The current through the resistors is:

• Current through 3Ω: $I = 1.622 , A$
• The current likewise branches into the parallel resistors (4Ω and 6Ω), which can be studied further if needed.