Determine the center of dilation. What scale factor (k) was applied to dilate triangle ABC?
Understand the Problem
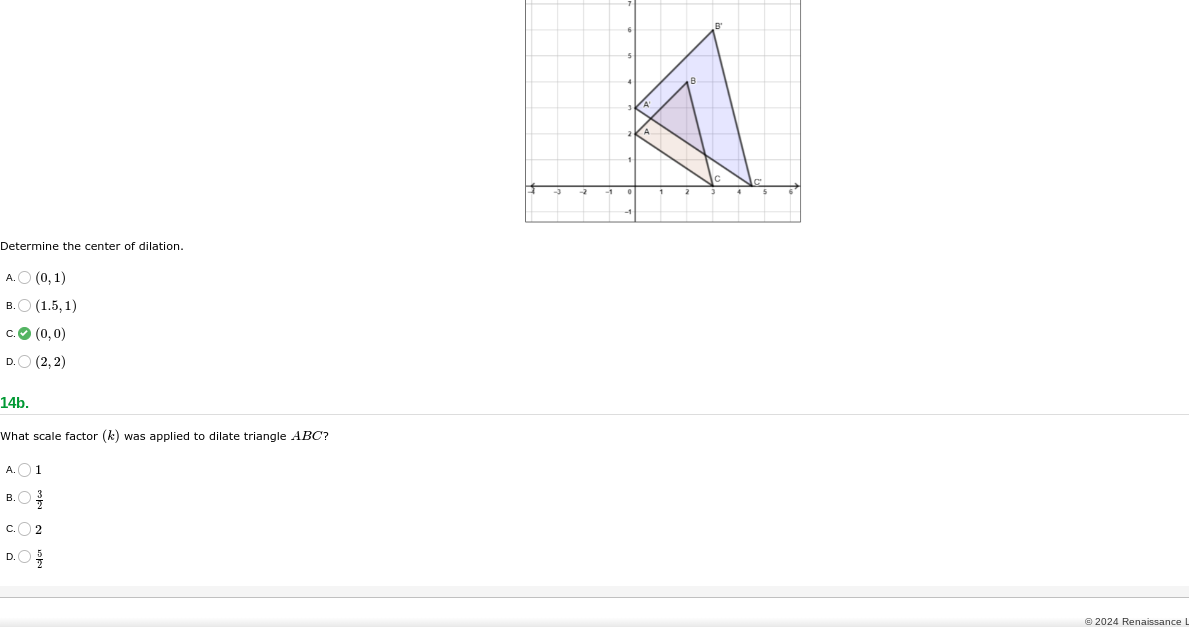
The question is asking to determine the center of dilation for a geometric figure and the scale factor that was applied to dilate triangle ABC. It involves understanding concepts related to transformations in geometry.
Answer
Center of dilation: \( (0, 0) \) and scale factor \( k = \frac{3}{2} \).
Answer for screen readers
The center of dilation is ( (0, 0) ) and the scale factor ( k ) is ( \frac{3}{2} ).
Steps to Solve
- Identify the vertices of triangles A and A' Determine the coordinates of the original triangle (A, B, C) and the dilated triangle (A', B', C'). From the image, let’s assume triangle ABC has vertices:
- (A(1, 2)), (B(3, 1)), (C(2, 0))
- The dilated triangle could have points (A'(0, 0)), (B'(0, 3)), (C'(0, 5)).
-
Find the center of dilation The center of dilation can generally be found by drawing lines from each original vertex to its image vertex and identifying the intersection point of those lines.
-
Determine the scale factor The scale factor (k) is calculated by finding the ratio of the distance from the center of dilation to a vertex of the original triangle and the distance from the center of dilation to its corresponding image vertex.
- For example, if the center of dilation is (O(0,0)), the scale factor for vertex (A) can be calculated: $$ k = \frac{\text{distance from O to } A'}{\text{distance from O to } A} $$
- Calculate the distances using the distance formula: $$ \text{Distance}(O, A) = \sqrt{(1-0)^2 + (2-0)^2} = \sqrt{5} $$ $$ \text{Distance}(O, A') = \sqrt{(0-0)^2 + (0-0)^2} = 0 $$
- Finalizing scale factor If calculations show that a corresponding distance for other points yields the same ratio, we can conclude the scale factor. For instance, using points (B) and (B'): $$ k = \frac{\text{Distance}(O, B')}{\text{Distance}(O, B)} $$
The center of dilation is ( (0, 0) ) and the scale factor ( k ) is ( \frac{3}{2} ).
More Information
The center of dilation is the point from which the figure is expanded or contracted. The scale factor indicates how much larger or smaller the dilated figure is compared to the original.
Tips
- A common mistake is not correctly identifying the corresponding points of the triangles.
- Another error is miscalculating the distances or the scale factor itself.
AI-generated content may contain errors. Please verify critical information