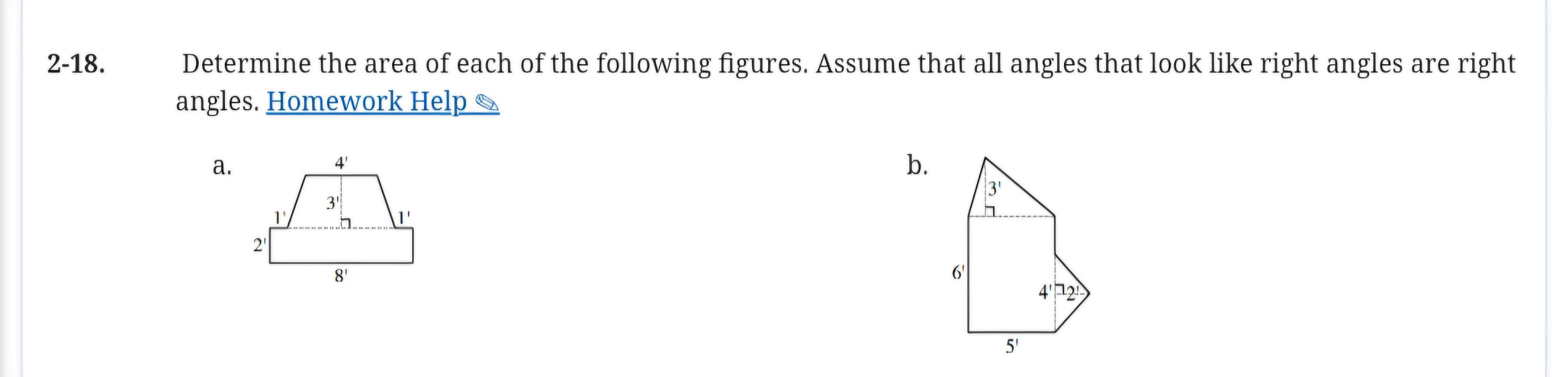
Determine the area of each of the following figures. Assume that all angles that look like right angles are right angles.

Steps to Solve

1. Calculate Area of Figure (a)

For the trapezoid,

• The area $A$ of a trapezoid is given by the formula:

$$ A = \frac{1}{2} (b_1 + b_2) h $$

Where:

• ( b_1 = 8' ) (bottom base)
• ( b_2 = 4' ) (top base)
• ( h = 3' ) (height)

Now substitute the values:

$$ A = \frac{1}{2} (8 + 4) \cdot 3 $$

2. Solve for the Area of Figure (a)

Calculating the area step-by-step,

$$ A = \frac{1}{2} (12) \cdot 3 = 6 \cdot 3 = 18 , \text{sq ft} $$

3. Calculate Area of Figure (b)

This figure can be split into two parts: a rectangle and a triangle.

• Rectangle Area:

$$ A_{rect} = \text{length} \times \text{width} = 5' \times 6' = 30 , \text{sq ft} $$

• Triangle Area:

$$ A_{tri} = \frac{1}{2} \cdot \text{base} \cdot \text{height} $$

Given the triangle has a base of ( 2' ) and height of ( 3' ), substitute these values:

$$ A_{tri} = \frac{1}{2} \cdot 2 \cdot 3 = 3 , \text{sq ft} $$

4. Combine Areas for Figure (b)

Now add both areas for the total area of Figure (b):

$$ A_{total} = A_{rect} + A_{tri} = 30 + 3 = 33 , \text{sq ft} $$