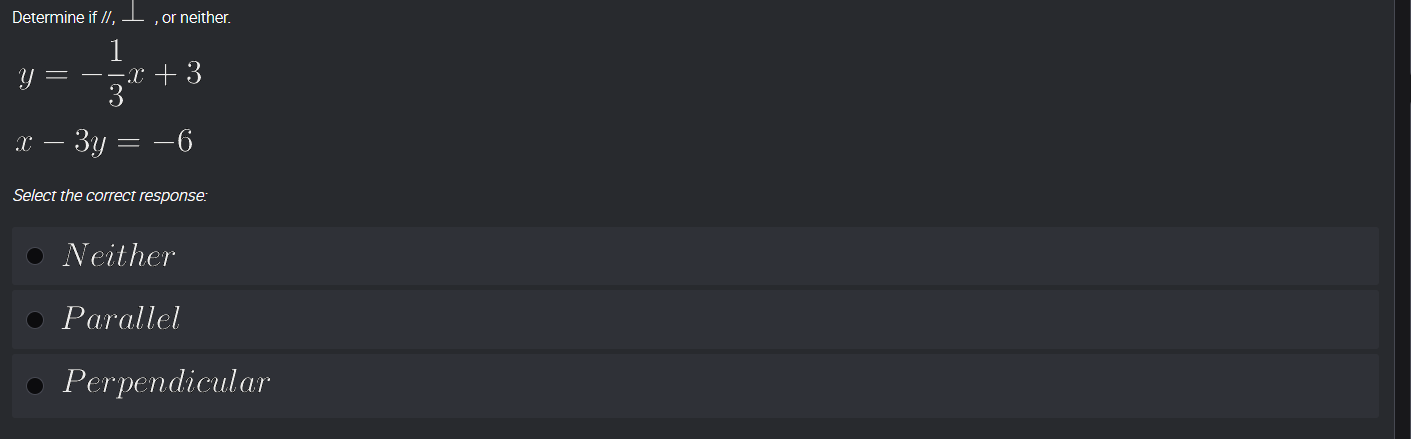
Determine if the two lines are parallel, perpendicular, or neither.
Understand the Problem
The question is asking to determine the relationship between two lines given in the forms of equations. This involves analyzing their slopes to determine if they are parallel, perpendicular, or neither.
Answer
Neither
Answer for screen readers
Neither
Steps to Solve
- Identify the slope of the first line
The first line is given in slope-intercept form: $$ y = -\frac{1}{3}x + 3 $$
Here, the slope $m_1$ of the first line is: $$ m_1 = -\frac{1}{3} $$
- Convert the second equation to slope-intercept form
The second equation is: $$ x - 3y = -6 $$
We can solve for $y$ to find the slope. Rearranging the equation, we get: $$ -3y = -x - 6 $$
Now, divide by -3: $$ y = \frac{1}{3}x + 2 $$
Thus, the slope $m_2$ of the second line is: $$ m_2 = \frac{1}{3} $$
- Determine the relationship between the slopes
Lines are:
- Parallel if their slopes are equal: $m_1 = m_2$.
- Perpendicular if the product of their slopes is -1: $m_1 \cdot m_2 = -1$.
Calculating the product of the slopes: $$ m_1 \cdot m_2 = \left(-\frac{1}{3}\right) \cdot \left(\frac{1}{3}\right) = -\frac{1}{9} $$
Since the slopes are not equal and their product is not -1, the lines are neither parallel nor perpendicular.
Neither
More Information
The first line has a slope of $-\frac{1}{3}$, while the second line has a slope of $\frac{1}{3}$. Their slopes indicate that they are neither parallel nor perpendicular.
Tips
- Confusing equality of slopes with the condition for perpendicular lines. Remember, slopes must either be equal for parallel or their product must equal -1 for perpendicular.
- Miscalculating the slope when converting from standard form to slope-intercept form. Always double-check your calculations.
AI-generated content may contain errors. Please verify critical information