Describe and correct the error in solving the linear system y = 2x - 1 and y = x + 1.
Understand the Problem
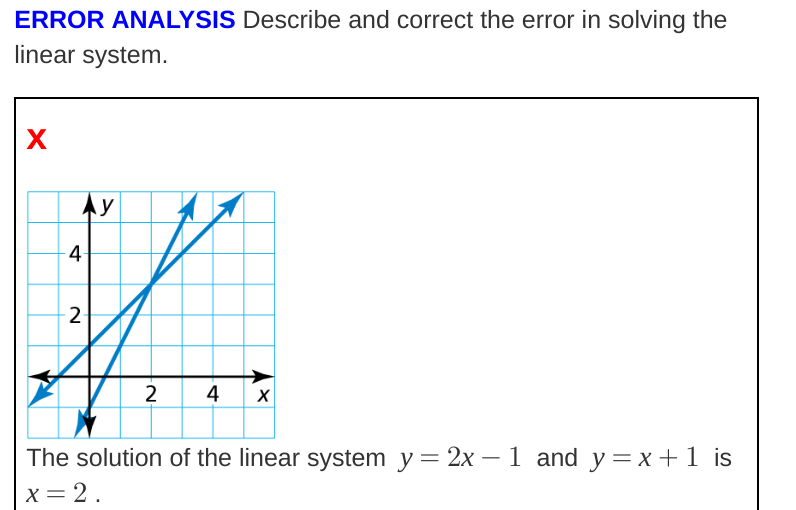
The question is asking to identify and correct the error in solving the given linear system represented graphically. The two equations given are y = 2x - 1 and y = x + 1, and the interpretation of their intersection is being questioned.
Answer
The solution to the linear system is \( (2, 3) \).
Answer for screen readers
The solution to the linear system is ( (2, 3) ).
Steps to Solve
-
Identify the given equations The linear equations provided are:
$$ y = 2x - 1 $$
$$ y = x + 1 $$ -
Graph the equations We can plot both equations on the graph.
For $y = 2x - 1$:
- When $x = 0$, $y = -1$ (point $(0, -1)$)
- When $x = 2$, $y = 3$ (point $(2, 3)$)
For $y = x + 1$:
- When $x = 0$, $y = 1$ (point $(0, 1)$)
- When $x = 2$, $y = 3$ (point $(2, 3)$)
-
Find the intersection point The two lines intersect at the point $(2, 3)$. Therefore, the correct solution to the system is determined by setting the equations equal to each other: $$ 2x - 1 = x + 1 $$
-
Solve for (x) Rearranging the equation gives: $$ 2x - x = 1 + 1 $$
Thus, $$ x = 2 $$ -
Determine (y) using either equation Substituting $x = 2$ into one of the equations, such as $y = x + 1$, gives: $$ y = 2 + 1 = 3 $$
-
Conclusion The solution to the system is the point $(2, 3)$, not just $x = 2$. The statement in the question incorrectly claims the solution is solely $x = 2$.
The solution to the linear system is ( (2, 3) ).
More Information
In solving systems of equations, the solution is typically represented as an ordered pair ((x, y)) indicating where the lines intersect. The given equations represent two lines with different slopes, hence one line will cross the other at a specific point.
Tips
- Claiming the solution as a single variable: It’s a common mistake to only state (x) without providing (y) in linear systems. Solutions should be given in the form of ordered pairs.
- Misinterpreting the graph: Always double-check the graph to ensure that the intersection point is correctly identified.
AI-generated content may contain errors. Please verify critical information