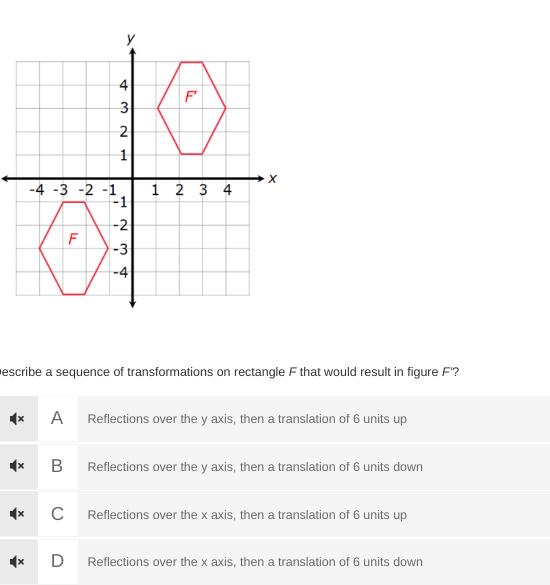
Describe a sequence of transformations on rectangle F that would result in figure F'?
Understand the Problem
The question is asking how to transform rectangle F to get figure F' by describing a specific sequence of operations on the shape. We need to identify the correct series of transformations, which could include reflections and translations.
Answer
Reflections over the y-axis, then a translation of 5 units up.
Answer for screen readers
The sequence of transformations is: Reflections over the y-axis, then a translation of 5 units up.
Steps to Solve
-
Identify the Initial Position of Rectangle F
Rectangle F is located between x-coordinates -4 and -1 and y-coordinates -4 and -1. -
Determine Figure F’ Position
Figure F' is positioned between x-coordinates 1 and 4, and y-coordinates 1 and 4. -
Analyze Required Transformations
To move from F to F', we can see that the shape must first be shifted from the left half to the right half of the coordinate plane. The movement from a negative x-position to a positive one indicates a reflection over the y-axis. -
Calculate the Translation
Starting from F at approximately the center (-2.5, -2.5), after reflecting, the shape would be located at (2.5, -2.5). To move to F', which is centered at (2.5, 2.5), a translation upwards by 5 units is needed. -
Combine the Transformations
Thus, the sequence includes a reflection over the y-axis followed by a translation of 5 units upwards.
The sequence of transformations is: Reflections over the y-axis, then a translation of 5 units up.
More Information
In this problem, transforming shapes often involves both reflections and translations on the Cartesian plane, requiring an understanding of how these transformations affect the coordinates of points in space.
Tips
- Confusing the direction of the reflection or translation.
- Forgetting to add the final translation distance after reflecting the shape.
AI-generated content may contain errors. Please verify critical information