Decide if the series sum from n=1 to infinity of (4^n - 3^n)^(1/n) converges or diverges.
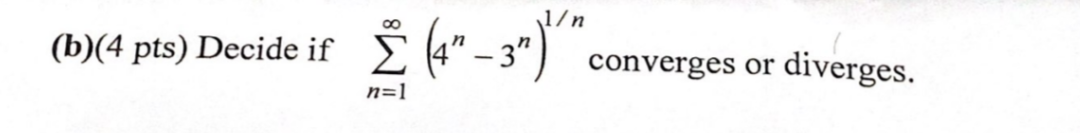
Understand the Problem
The question asks us to determine whether the infinite series ( \sum_{n=1}^{\infty} \left(4^n - 3^n \right)^{\frac{1}{n}} ) converges or diverges. This involves analyzing the behavior of the terms as ( n ) approaches infinity.
Answer
The series diverges.
Answer for screen readers
The series ( \sum_{n=1}^{\infty} \left(4^n - 3^n \right)^{\frac{1}{n}} ) diverges.
Steps to Solve
- Identify the general term of the series
The given series is
$$ \sum_{n=1}^{\infty} \left(4^n - 3^n \right)^{\frac{1}{n}} $$
This means our general term ( a_n ) is
$$ a_n = \left(4^n - 3^n \right)^{\frac{1}{n}} $$
- Simplify the term as ( n ) approaches infinity
As ( n \to \infty ), we can simplify
$$ 4^n - 3^n \approx 4^n $$
because ( 4^n ) grows much faster than ( 3^n ).
Thus,
$$ a_n \approx \left(4^n\right)^{\frac{1}{n}} = 4 $$
- Analyze the behavior of ( a_n )
From the simplification, we conclude:
$$ \lim_{n \to \infty} a_n = 4 \quad \text{(as ( n \to \infty ))} $$
This indicates that the terms do not approach zero.
- Apply the Divergence Test
The Divergence Test states that if
$$ \lim_{n \to \infty} a_n \neq 0 $$
then the series diverges.
Since ( \lim_{n \to \infty} a_n = 4 \neq 0 ), we conclude that the series diverges.
The series ( \sum_{n=1}^{\infty} \left(4^n - 3^n \right)^{\frac{1}{n}} ) diverges.
More Information
This result is consistent with the Divergence Test in calculus, which states that if the limit of the terms of a series does not approach zero, the series must diverge.
Tips
- Misapplying the limit by failing to correctly evaluate ( 4^n - 3^n ) as ( n \to \infty ). Always compare leading terms.
- Assuming that just because ( a_n ) is large for large ( n ), the series converges. Remember to consider the limit!
AI-generated content may contain errors. Please verify critical information