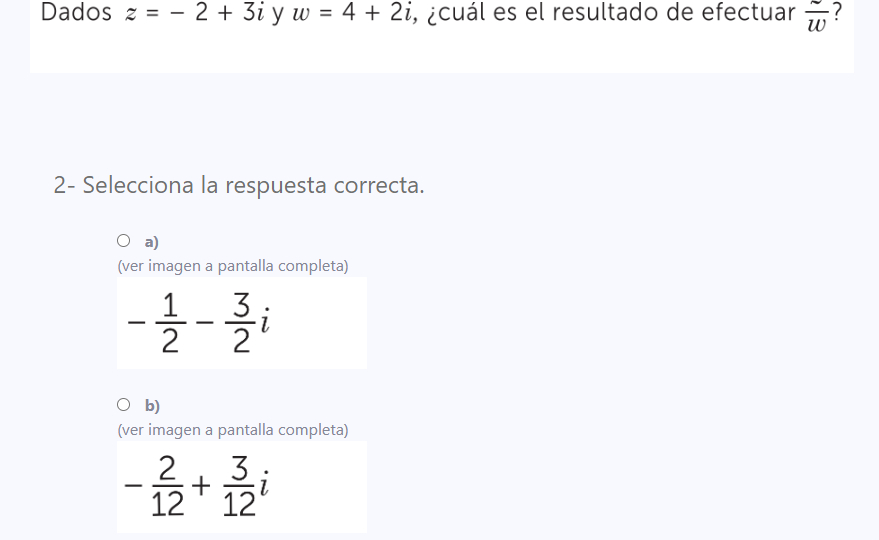
Dados z = -2 + 3i y w = 4 + 2i, ¿cuál es el resultado de efectuar w̅?

Steps to Solve

1. Identificar los números complejos

Dado que ( z = -2 + 3i ) y ( w = 4 + 2i ), primero identificamos las partes real e imaginaria.

2. Calcular la conjugada de ( w )

La conjugada de un número complejo ( a + bi ) se obtiene cambiando el signo de la parte imaginaria. Por lo tanto, la conjugada de ( w = 4 + 2i ) es: $$ \overline{w} = 4 - 2i $$

3. Dividir ( \overline{w} ) por ( z )

Para encontrar ( \frac{\overline{w}}{z} ), sustituimos ( \overline{w} ) y ( z ): $$ \frac{4 - 2i}{-2 + 3i} $$

4. Multiplicar por el conjugado del denominador

Multiplicamos el numerador y el denominador por el conjugado del denominador ( -2 - 3i ): $$ \frac{(4 - 2i)(-2 - 3i)}{(-2 + 3i)(-2 - 3i)} $$

5. Calcular el denominador

Calculamos el denominador usando la fórmula ( (a + bi)(a - bi) = a^2 + b^2 ): $$ (-2)^2 + (3)^2 = 4 + 9 = 13 $$

6. Calcular el numerador

Expandimos el numerador: $$ (4)(-2) + (4)(-3i) + (-2i)(-2) + (-2i)(-3i) = -8 - 12i + 4i + 6 = -2 - 8i $$

7. Combinar resultados

Juntando todo, obtenemos: $$ \frac{-2 - 8i}{13} = -\frac{2}{13} - \frac{8}{13}i $$