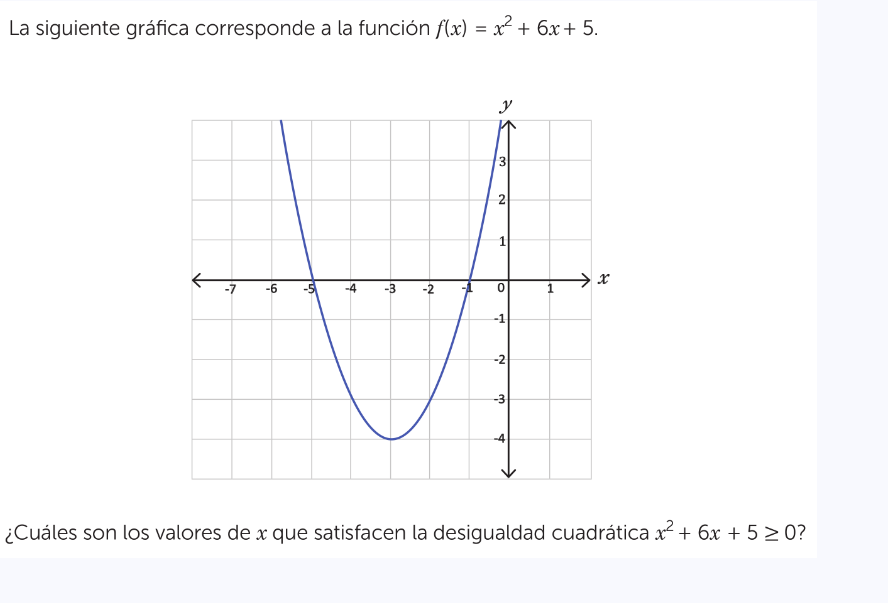
¿Cuáles son los valores de x que satisfacen la desigualdad cuadrática x² + 6x + 5 ≥ 0?

Steps to Solve

1. Identificar la función cuadrática La función dada es $f(x) = x^2 + 6x + 5$. Esta es una parábola que abre hacia arriba.

2. Encontrar las raíces de la función Para resolver la desigualdad $x^2 + 6x + 5 ≥ 0$, primero encontramos las raíces de la ecuación $x^2 + 6x + 5 = 0$.

Usamos la fórmula cuadrática:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

donde $a = 1$, $b = 6$, y $c = 5$.

Sustituyendo los valores:

$$x = \frac{-6 \pm \sqrt{6^2 - 4 \cdot 1 \cdot 5}}{2 \cdot 1}$$

3. Calcular el discriminante Calculamos el discriminante:

$$6^2 - 4 \cdot 1 \cdot 5 = 36 - 20 = 16$$

4. Encontrar las raíces Ahora, calculamos las raíces con el discriminante:

$$x = \frac{-6 \pm \sqrt{16}}{2}$$

Esto nos dará:

$$x = \frac{-6 \pm 4}{2}$$

5. Listar las raíces Resolviendo, obtenemos:

$$x_1 = \frac{-2}{2} = -1 \quad \text{y} \quad x_2 = \frac{-10}{2} = -5$$

6. Analizar la desigualdad La función cuadrática es positiva o igual a cero fuera de los intervalos definidos por las raíces.

Los intervalos son:

• $(-\infty, -5]$
• $[-1, \infty)$

7. Conclusión Los valores de $x$ que satisfacen la desigualdad son:

$$x \leq -5 \quad \text{o} \quad x \geq -1$$