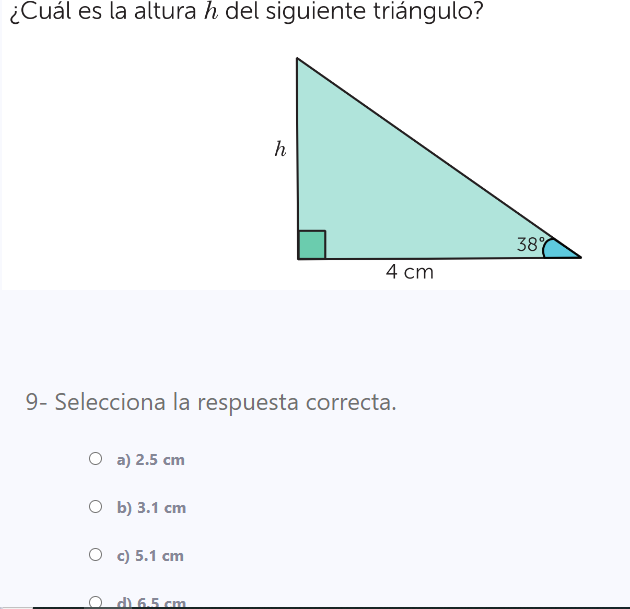
¿Cuál es la altura h del siguiente triángulo?
Understand the Problem
La pregunta está pidiendo calcular la altura h de un triángulo rectángulo, utilizando la información proporcionada sobre un lado y un ángulo.
Answer
$3.1 \text{ cm}$
Answer for screen readers
La altura $h$ del triángulo es aproximadamente $3.1$ cm.
Steps to Solve
- Identificar las funciones trigonométricas Para encontrar la altura $h$ del triángulo, podemos usar la función trigonométrica que relaciona un ángulo y las longitudes de los lados. En este caso, usaremos la función $\tan$ (tangente), que se define como:
$$ \tan(\theta) = \frac{\text{opuesto}}{\text{adyacente}} $$
- Aplicar la función tangente En nuestro triángulo, el ángulo es $38^\circ$, el lado opuesto es la altura $h$, y el lado adyacente es la base de $4$ cm. Por lo tanto, la relación se puede expresar como:
$$ \tan(38^\circ) = \frac{h}{4} $$
- Despejar la altura $h$ Multiplicamos ambos lados de la ecuación por $4$ para despejar $h$:
$$ h = 4 \cdot \tan(38^\circ) $$
- Calcular $h$ usando una calculadora Finalmente, obtenemos el valor de $h$: Primero, calculamos $\tan(38^\circ)$ y luego multiplicamos por 4:
$$ h \approx 4 \cdot 0.7813 \approx 3.1252 $$
La altura $h$ del triángulo es aproximadamente $3.1$ cm.
More Information
La tangente de un ángulo en un triángulo rectángulo relaciona la longitud del lado opuesto con la longitud del lado adyacente. Esto es útil en problemas de triángulos para encontrar longitudes desconocidas.
Tips
- Olvidar convertir el ángulo de grados a radianes: En algunas calculadoras, asegúrate de que estás en la configuración correcta (grados).
- Confundir el lado opuesto con el lado adyacente: Asegúrate de identificar correctamente los lados en relación con el ángulo dado.
AI-generated content may contain errors. Please verify critical information