∫ cot(θ) dθ
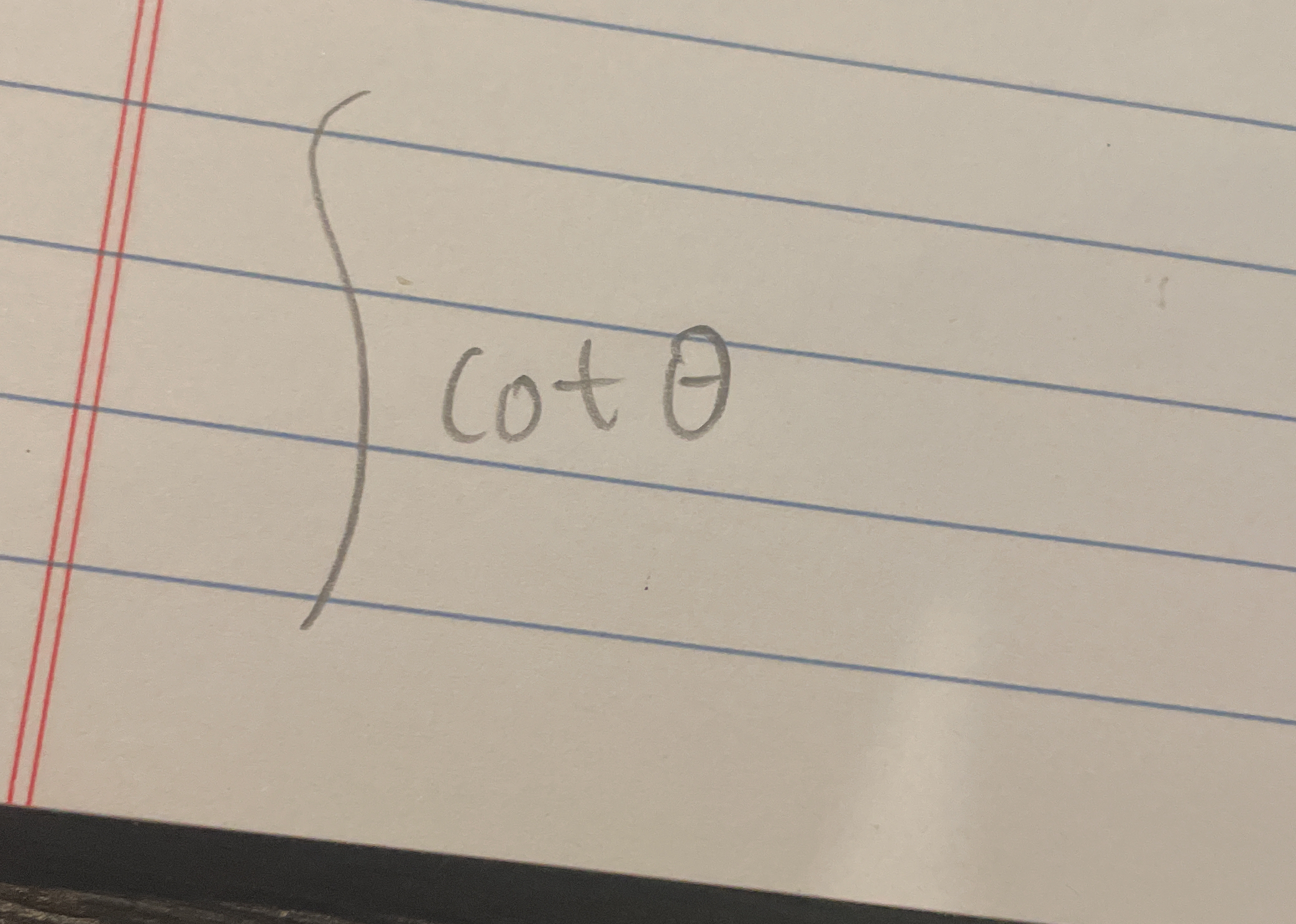
Understand the Problem
The question appears to be asking for the integral of cotangent with respect to theta, which is a common calculus exercise.
Answer
$$ \int \cot(\theta) \, d\theta = \ln|\sin(\theta)| + C $$
Answer for screen readers
$$ \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C $$
Steps to Solve
- Recall the formula for integration of cotangent
The integral of the cotangent function can be expressed as: $$ \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C $$ where $C$ is the constant of integration.
- Substitute the variable
In our case, we are integrating $\cot(\theta)$ with respect to $\theta$, so we can directly apply the formula: $$ \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C $$
- Write down the final result
Thus, the solution to the integral can be stated clearly as: $$ \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C $$
$$ \int \cot(\theta) , d\theta = \ln|\sin(\theta)| + C $$
More Information
The integral of cotangent is a fundamental formula in calculus. It shows the relationship between cotangent and the logarithm of sine. This integral is useful in solving various problems, particularly in trigonometry and calculus.
Tips
- Forgetting to include the constant of integration $C$.
- Confusing the integral of cotangent with that of tangent, which has a different result.
- Neglecting the absolute value in the logarithmic function.
AI-generated content may contain errors. Please verify critical information