cot(4n) + sin(5n)/2
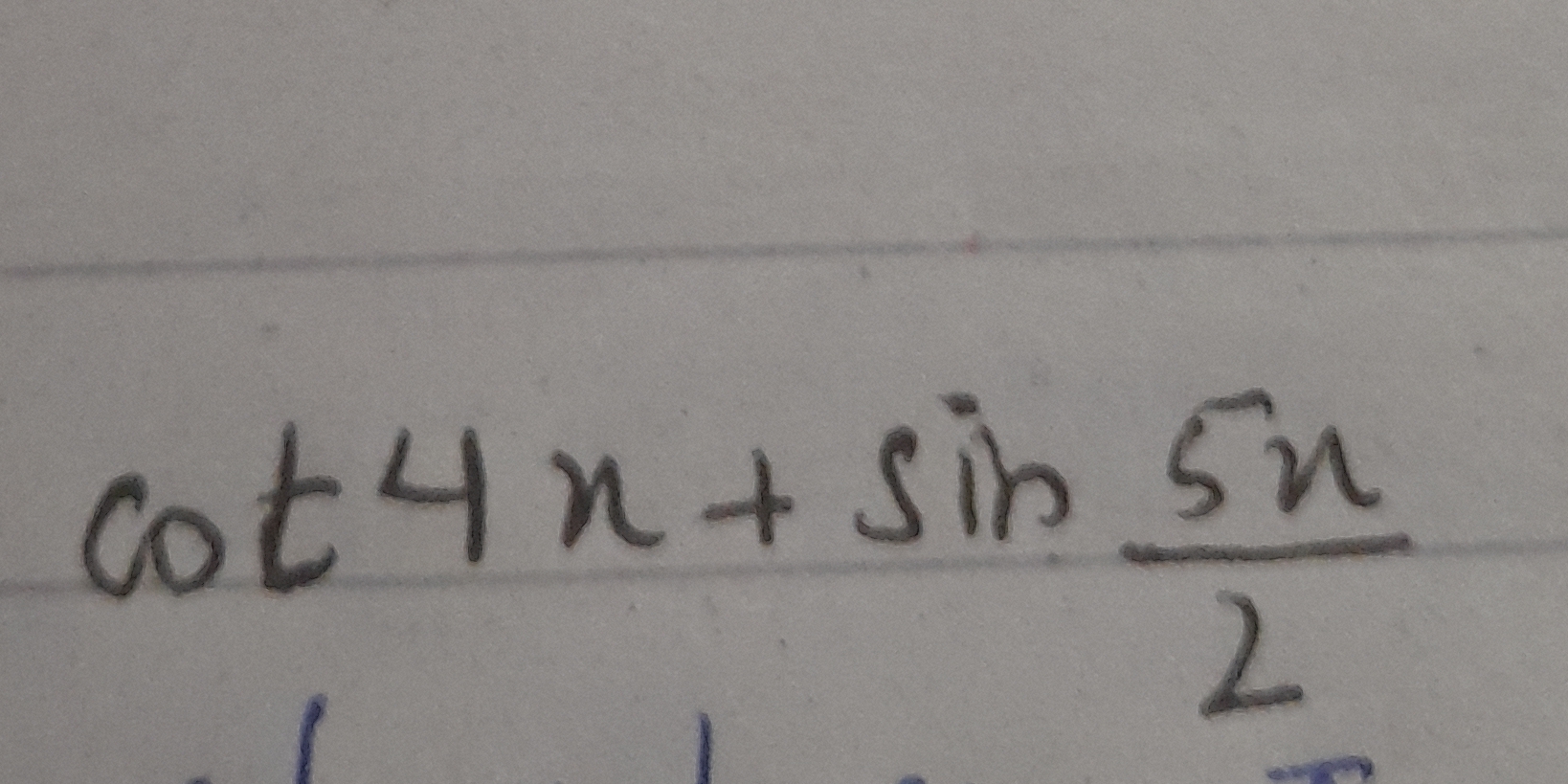
Understand the Problem
The question appears to involve a mathematical expression that includes trigonometric functions, specifically cotangent and sine, likely pertaining to an equation or identity involving these functions.
Answer
The simplified expression is \( \frac{2\cos(4n) + \sin(5n)\sin(4n)}{2\sin(4n)} \).
Answer for screen readers
The expression simplifies to: $$ \frac{2\cos(4n) + \sin(5n)\sin(4n)}{2\sin(4n)} $$
Steps to Solve
-
Identify the Expression The given expression is ( \cot(4n) + \frac{\sin(5n)}{2} ).
-
Understanding Cotangent Recall that the cotangent function is the reciprocal of the tangent function: $$ \cot(x) = \frac{1}{\tan(x)} = \frac{\cos(x)}{\sin(x)} $$ This means you can rewrite ( \cot(4n) ) in terms of sine and cosine: $$ \cot(4n) = \frac{\cos(4n)}{\sin(4n)} $$
-
Combine the Terms Now the expression can be summed up: $$ \frac{\cos(4n)}{\sin(4n)} + \frac{\sin(5n)}{2} $$
-
Simplifying the Expression (if needed) If simplification is desired, find a common denominator and combine: $$ \frac{2\cos(4n)}{2\sin(4n)} + \frac{\sin(5n)\sin(4n)}{2\sin(4n)} = \frac{2\cos(4n) + \sin(5n)\sin(4n)}{2\sin(4n)} $$
The expression simplifies to: $$ \frac{2\cos(4n) + \sin(5n)\sin(4n)}{2\sin(4n)} $$
More Information
This expression combines trigonometric identities, and understanding the behavior of these functions is key, especially when dealing with angles in multiple dimensions. The result shows how cotangent can integrate smoothly with sine functions through mutual terms.
Tips
- Confusing cotangent with tangent: Remember, ( \cotangent ) is the reciprocal of ( \tan ).
- Forgetting to correctly apply the sine identities or miscalculating them.
AI-generated content may contain errors. Please verify critical information