Convert from standard form to vertex (graphing) y = x^2 + 8x + 11.
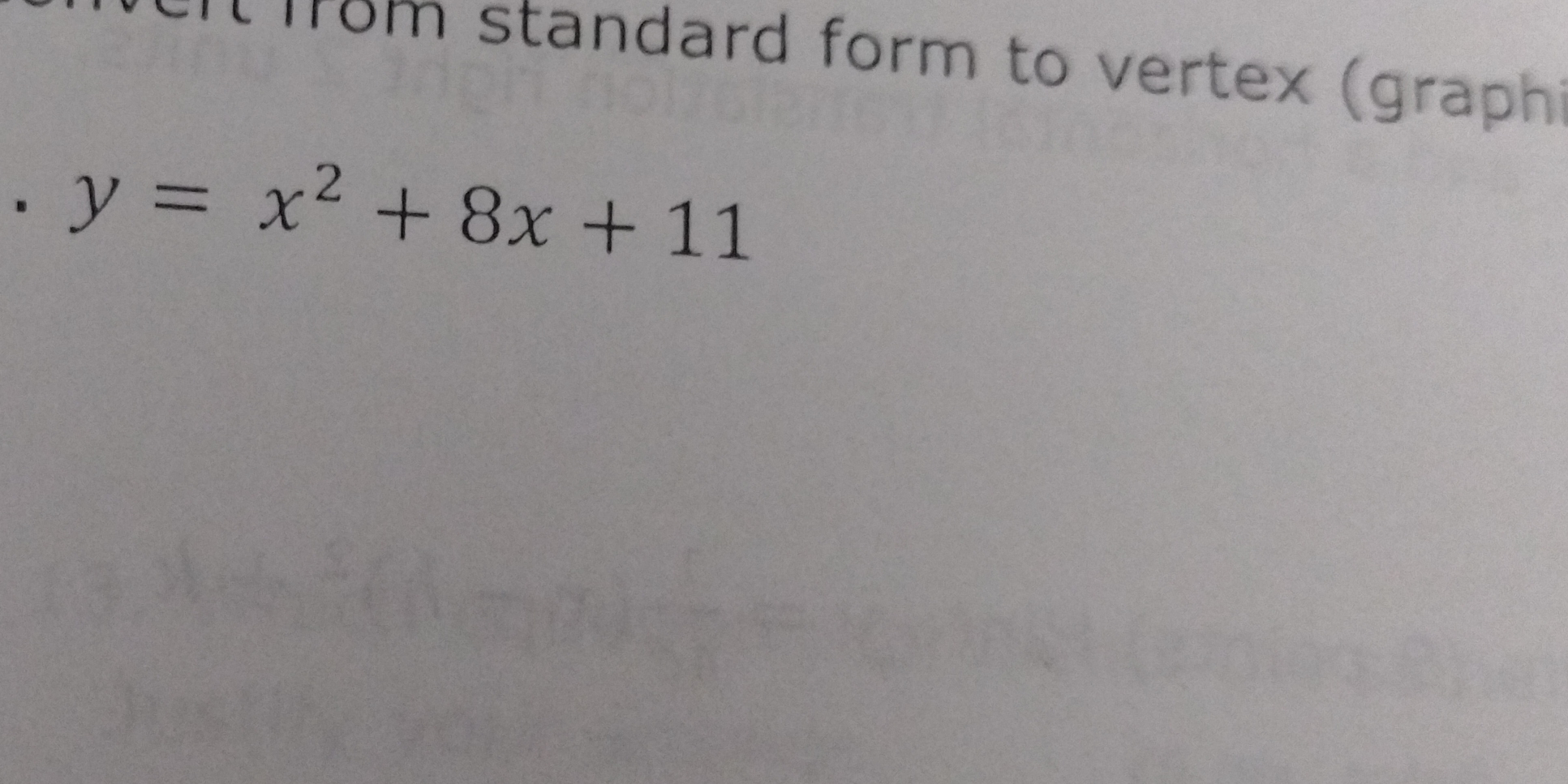
Understand the Problem
The question is requesting to convert the given quadratic equation from standard form to vertex form in order to identify its vertex and possibly graph it.
Answer
The vertex form of the equation is $$ y = (x + 4)^2 - 5 $$.
Answer for screen readers
The vertex form of the equation is: $$ y = (x + 4)^2 - 5 $$
Steps to Solve
-
Identify the standard form The given equation is in standard form:
$$ y = x^2 + 8x + 11 $$ -
Complete the square To convert to vertex form, we need to complete the square. Start with the $x$ terms:
- Take half of the coefficient of $x$ (which is 8), square it: $$ \left(\frac{8}{2}\right)^2 = 16 $$
- Rewrite the equation Now we can rewrite the quadratic:
- Add and subtract 16 inside the equation: $$ y = (x^2 + 8x + 16) - 16 + 11 $$
- This simplifies to: $$ y = (x + 4)^2 - 5 $$
- Express in vertex form Now we have the vertex form: $$ y = (x + 4)^2 - 5 $$ Here, the vertex is at $(-4, -5)$.
The vertex form of the equation is: $$ y = (x + 4)^2 - 5 $$
More Information
In vertex form, the vertex of the parabola can be easily identified as the point where the graph changes direction. In this case, the vertex is at the point $(-4, -5)$, which represents the minimum point of the parabola.
Tips
- Forgetting to both add and subtract the squared term while completing the square, which can alter the equation.
- Miscalculating half of the $x$ coefficient, which leads to an incorrect completed square.
AI-generated content may contain errors. Please verify critical information