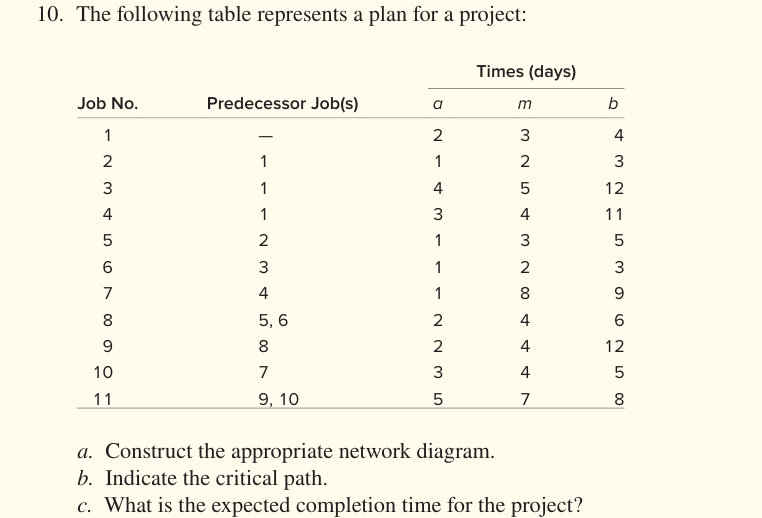
Construct the appropriate network diagram. Indicate the critical path. What is the expected completion time for the project?

Steps to Solve

1. Identify Activities and Predecessors
   From the provided table, list all the jobs and their predecessors. Each job's completion depends on its predecessors.

   • Job 1: No predecessors
   • Job 2: Predecessor - Job 1
   • Job 3: Predecessor - Job 1
   • Job 4: Predecessor - Job 1
   • Job 5: Predecessor - Job 2
   • Job 6: Predecessor - Job 3
   • Job 7: Predecessor - Job 4
   • Job 8: Predecessors - Jobs 5 and 6
   • Job 9: Predecessor - Job 8
   • Job 10: Predecessor - Job 7
   • Job 11: Predecessors - Jobs 9 and 10

2. Construct the Network Diagram
   Create a visual representation based on the job dependencies.

   • Each job is a node. Draw directed edges from predecessors to their successors.
   • The diagram starts from Job 1 and follows through to Job 11, laying out the flow of activities.

3. Calculate Expected Time for Each Activity
   Use the formula for the expected time ((TE)) for each job:
   $$ TE = \frac{a + 4m + b}{6} $$ where (a) is the optimistic time, (m) is the most likely time, and (b) is the pessimistic time.

   • Calculate (TE) for each job:
   • Job 1: ( TE_1 = \frac{2 + 4 \cdot 3 + 4}{6} = 3.33 )
   • Job 2: ( TE_2 = \frac{1 + 4 \cdot 2 + 3}{6} = 2.33 )
   • Job 3: ( TE_3 = \frac{4 + 4 \cdot 5 + 12}{6} = 6.33 )
   • Job 4: ( TE_4 = \frac{3 + 4 \cdot 4 + 11}{6} = 5.33 )
   • Job 5: ( TE_5 = \frac{1 + 4 \cdot 3 + 5}{6} = 3.00 )
   • Job 6: ( TE_6 = \frac{1 + 4 \cdot 2 + 3}{6} = 2.00 )
   • Job 7: ( TE_7 = \frac{1 + 4 \cdot 8 + 9}{6} = 6.00 )
   • Job 8: ( TE_8 = \frac{2 + 4 \cdot 4 + 6}{6} = 4.00 )
   • Job 9: ( TE_9 = \frac{2 + 4 \cdot 4 + 12}{6} = 6.00 )
   • Job 10: ( TE_{10} = \frac{3 + 4 \cdot 4 + 5}{6} = 4.33 )
   • Job 11: ( TE_{11} = \frac{5 + 4 \cdot 7 + 8}{6} = 6.67 )

4. Determine the Critical Path
   Identify the longest path through the network diagram by summing the expected times of the activities in each path.

   • Examine each route:

   • Paths:

     • ( 1 \to 2 \to 5 \to 8 \to 9 \to 11 )
     • ( 1 \to 3 \to 6 \to 8 \to 9 \to 11 )
     • ( 1 \to 4 \to 7 \to 10 \to 11 )

   • Critical Path: The longest time from start to end, which yields the project's total duration.

5. Calculate Expected Completion Time
   Add the expected times of activities on the critical path.

   • For example, if the critical path is ( 1 \to 2 \to 5 \to 8 \to 9 \to 11 ):
   • ( TE_{total} = TE_1 + TE_2 + TE_5 + TE_8 + TE_9 + TE_{11} )
   • Calculate as necessary based on the actual critical path determined.