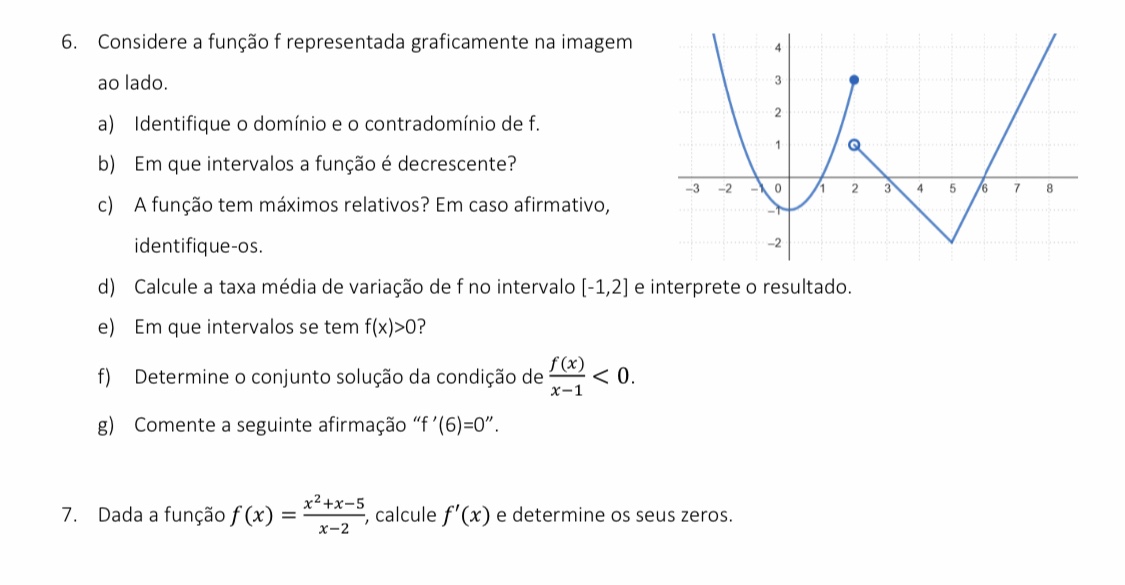
Considere a função f representada graficamente na imagem ao lado. a) Identifique o domínio e o contradomínio de f. b) Em que intervalos a função é decrescente? c) A função tem máxi... Considere a função f representada graficamente na imagem ao lado. a) Identifique o domínio e o contradomínio de f. b) Em que intervalos a função é decrescente? c) A função tem máximos relativos? Em caso afirmativo, identifique-os. d) Calcule a taxa média de variação de f no intervalo [-1,2] e interprete o resultado. e) Em que intervalos se tem f(x)>0? f) Determine o conjunto solução da condição de f(x)/(x-1) < 0. g) Comente a seguinte afirmação 'f'(6)=0'. 7. Dada a função f(x) = (x^2+x-5)/(x-2), calcule f'(x) e determine os seus zeros.
Understand the Problem
A pergunta envolve análise de uma função, solicitando que se identifiquem várias características. Isso inclui o domínio e contradomínio, os intervalos de decrescimento, a identificação de máximos relativos, o cálculo da taxa média de variação em um intervalo específico, a análise dos intervalos em que a função é positiva e a determinação de condições específicas. Por fim, também pede o cálculo da derivada de uma função dada e a determinação de seus zeros.
Answer
Domínio: \( \mathbb{R} \), Contradomínio: \( [-2, +\infty) \), Decrescimento: \( (-\infty, -1) \) e \( (1, 2.5) \), Máximos: \( x = -1, 2.5 \), Taxa média: -1, \( f(x) > 0 \): \( (-\infty, -1) \) e \( (2, +\infty) \), Solução: \( (1, 2) \), Derivada: use a regra do quociente.
Answer for screen readers
-
Domínio: ( \mathbb{R} )
Contradomínio: ( [-2, +\infty) ) -
Intervalos de decrescimento: ( (-\infty, -1) ) e ( (1, 2.5) )
-
Máximos relativos: ( x = -1 ) e ( x \approx 2.5 )
-
Taxa média de variação: ( -1 )
-
Intervalos onde ( f(x) > 0 ): ( (-\infty, -1) ) e ( (2, +\infty) )
-
Conjunto solução para ( \frac{f(x)}{x-1} < 0 ): ( (1, 2) )
-
Cálculo de ( f'(x) ): ( \frac{(x-2)(2x+1)-(x^2+x-5)}{(x-2)^2} )
Steps to Solve
- Identificação do domínio e contradomínio
O domínio da função ( f(x) ) é o conjunto de todos os valores de ( x ) que podem ser utilizados. Portanto, pela observação do gráfico, podemos ver que a função está definida para todos os números reais, então o domínio é ( \mathbb{R} ).
O contradomínio é o conjunto de todos os valores que a função pode assumir. Pelo gráfico, a função atinge um valor mínimo de -2 e não tem um valor máximo, então o contradomínio é ( [-2, +\infty) ).
- Intervalos de decrescimento
Para identificar onde a função é decrescente, analisamos o gráfico. A função parece decrescer em dois intervalos:
- De ( -\infty ) até ( -1 ) (a função vai de valores altos para valores baixos).
- De ( 1 ) até ( 2.5 ) aproximadamente.
- Máximos relativos
A função tem máximos relativos em ( x = -1 ) e ( x = 2.5 ) aproximadamente, onde a curva atinge seu pico antes de descer. Esses pontos são identificados pela inclinação da curva mudando de positiva para negativa.
- Taxa média de variação em [-1, 2]
A taxa média de variação é dada pela fórmula:
$$ \text{Taxa média} = \frac{f(b) - f(a)}{b - a} $$
onde ( a = -1 ) e ( b = 2 ). Calculamos ( f(-1) = 3 ) e ( f(2) = 0 ):
$$ \text{Taxa média} = \frac{0 - 3}{2 - (-1)} = \frac{-3}{3} = -1 $$
A interpretação é que, em média, a função decresce a uma taxa de 1 unidade por cada unidade de ( x ).
- Intervalos onde ( f(x) > 0 )
Analisando o gráfico, a função é positiva nos intervalos onde está acima do eixo ( x ). Assim, ( f(x) > 0 ) ocorre em:
- ( (-\infty, -1) )
- ( (2, +\infty) )
- Conjunto solução para ( \frac{f(x)}{x-1} < 0 )
Para que essa fração seja negativa, precisamos que ( f(x) ) e ( x-1 ) tenham sinais opostos. A análise mostra que a função é negativa entre os intervalos ( (1, 2) ), enquanto ( x - 1 < 0 ) para ( x < 1 ). Isso implica que a solução está nos intervalos:
- ( (1, 2) )
- Cálculo da derivada ( f'(x) ) e seus zeros
Para a função dada ( f(x) = \frac{x^2 + x - 5}{x - 2} ), utilizaremos a regra do quociente.
A derivada é dada por:
$$ f'(x) = \frac{(x - 2)(2x + 1) - (x^2 + x - 5)}{(x - 2)^2} $$
Calculando ( f'(x) ) e igualando a zero para encontrar os zeros da função.
-
Domínio: ( \mathbb{R} )
Contradomínio: ( [-2, +\infty) ) -
Intervalos de decrescimento: ( (-\infty, -1) ) e ( (1, 2.5) )
-
Máximos relativos: ( x = -1 ) e ( x \approx 2.5 )
-
Taxa média de variação: ( -1 )
-
Intervalos onde ( f(x) > 0 ): ( (-\infty, -1) ) e ( (2, +\infty) )
-
Conjunto solução para ( \frac{f(x)}{x-1} < 0 ): ( (1, 2) )
-
Cálculo de ( f'(x) ): ( \frac{(x-2)(2x+1)-(x^2+x-5)}{(x-2)^2} )
More Information
O domínio e contradomínio fornecem informações essenciais sobre os valores que a função pode assumir, enquanto a taxa média de variação oferece uma visão sobre o comportamento geral da função em um intervalo específico. A derivada é uma ferramenta fundamental para entender a inclinação da função.
Tips
- Erros na identificação de máximos relativos, principalmente por não perceber corretamente a mudança na inclinação da função.
- Confundir intervalos de decrescimento com intervalos onde a função é negativa.
- Erros de cálculo ao aplicar a fórmula da taxa média de variação.
AI-generated content may contain errors. Please verify critical information