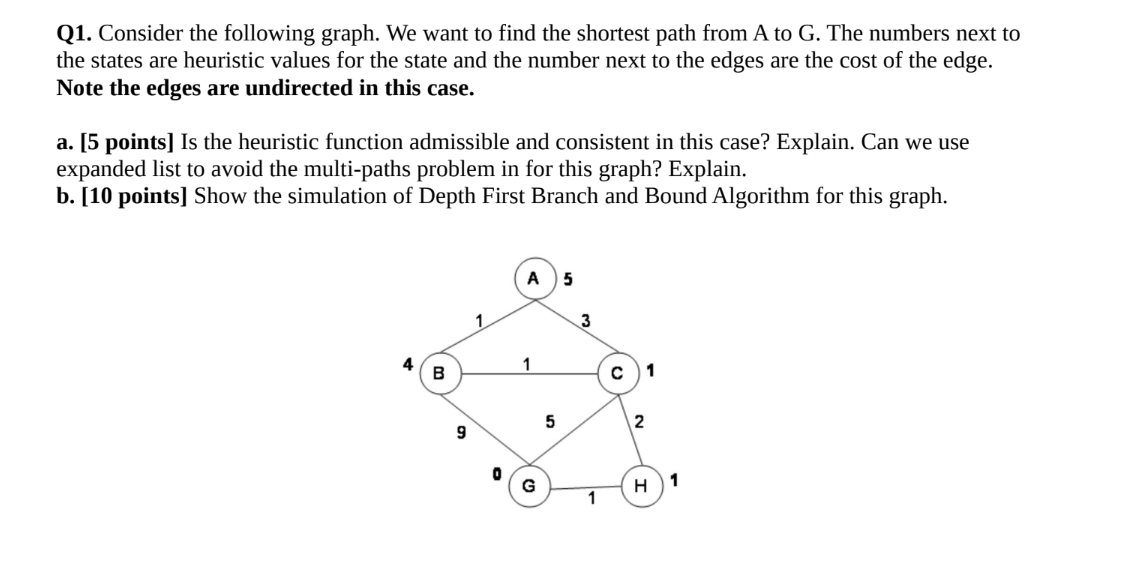
Consider the following graph. We want to find the shortest path from A to G. The numbers next to the states are heuristic values for the state and the number next to the edges are... Consider the following graph. We want to find the shortest path from A to G. The numbers next to the states are heuristic values for the state and the number next to the edges are the cost of the edge. Note the edges are undirected in this case. a. Is the heuristic function admissible and consistent in this case? Explain. Can we use an expanded list to avoid the multi-paths problem for this graph? Explain. b. Show the simulation of Depth First Branch and Bound Algorithm for this graph.
Understand the Problem
The question asks about finding the shortest path in a graph, specifically focusing on the admissibility and consistency of a heuristic function, as well as the simulation of the Depth First Branch and Bound Algorithm. It requires understanding graph theory concepts and algorithms.
Answer
a. Check admissibility and consistency for heuristic; expanded list prevents multipaths. b. Depth First Branch and Bound explores paths, updating minimum found cost.
a. The heuristic function is admissible if for each node, the heuristic value does not overestimate the shortest path cost to the goal. It is consistent if for each edge, the heuristic value decreases by at most the edge cost. Based on the graph information, check both properties for correctness. Using an expanded list allows the algorithm to avoid reconsidering nodes that have already been expanded, thus preventing cycles and redundant path searches.
b. Begin depth-first exploration from A, keeping track of the current path cost. When reaching G, compare path cost to any previously found best path, updating as necessary. Mark nodes as expanded to avoid revisits.
Answer for screen readers
a. The heuristic function is admissible if for each node, the heuristic value does not overestimate the shortest path cost to the goal. It is consistent if for each edge, the heuristic value decreases by at most the edge cost. Based on the graph information, check both properties for correctness. Using an expanded list allows the algorithm to avoid reconsidering nodes that have already been expanded, thus preventing cycles and redundant path searches.
b. Begin depth-first exploration from A, keeping track of the current path cost. When reaching G, compare path cost to any previously found best path, updating as necessary. Mark nodes as expanded to avoid revisits.
More Information
An admissible heuristic never overestimates the cost to reach the goal, which ensures optimality when finding shortest paths. Consistency, or the triangle inequality, ensures that the heuristic values sensibly propagate across the graph, maintaining efficiency.
Tips
Common mistakes include assuming permissive heuristics are consistent, overlooking specific edge costs, or neglecting to track expanded states, leading to infinite loops.
Sources
- Lecture 4: Optimal and Heuristic Search - ics.uci.edu
- Problem 1 – Search - ocw.mit.edu
AI-generated content may contain errors. Please verify critical information