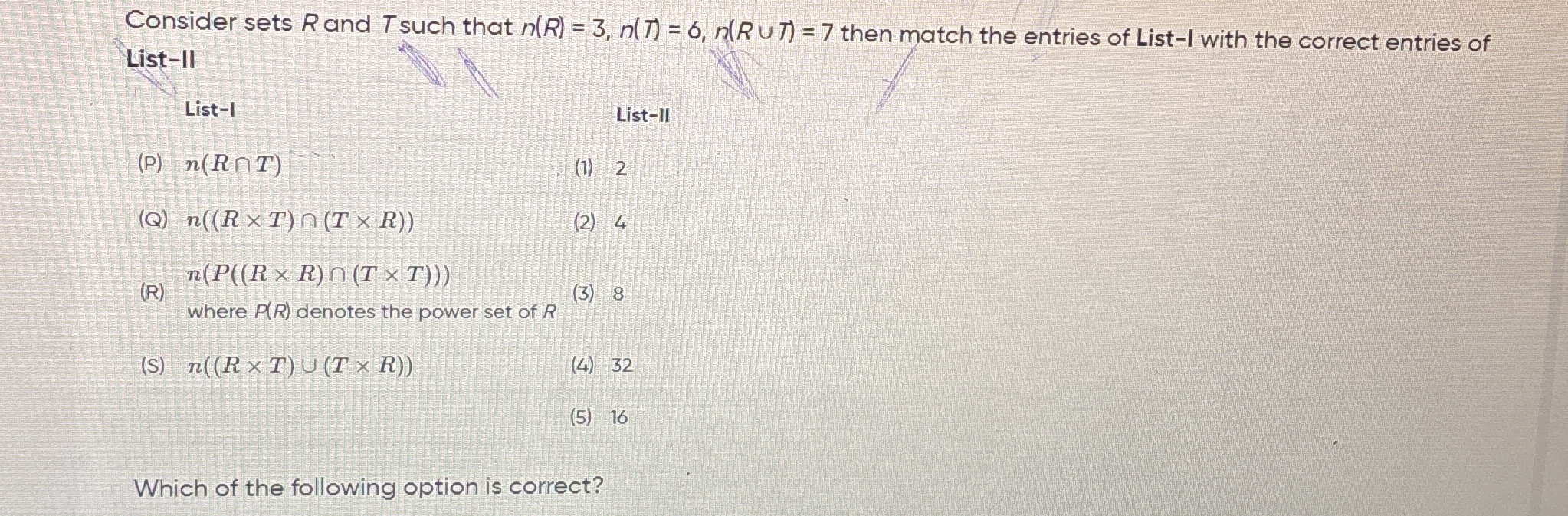
Consider sets R and T such that n(R) = 3, n(T) = 6, n(R ∪ T) = 7. Then match the entries of List-I with the correct entries of List-II. Which of the following options is correct?

Steps to Solve

1. Find $n(R ∩ T)$

   We can use the formula for the union of two sets:

   $$ n(R \cup T) = n(R) + n(T) - n(R \cap T) $$

   Substituting the known values:

   $$ 7 = 3 + 6 - n(R \cap T) $$

   Rearranging gives:

   $$ n(R \cap T) = 3 + 6 - 7 = 2. $$

2. Calculate $n((R × T) ∩ (T × R))$

   The Cartesian products $R \times T$ and $T \times R$ yield pairs from both sets. Their intersection $n((R \times T) \cap (T \times R))$ consists of pairs $(a, b)$ such that $a \in R$, $b \in T$ and vice versa. The intersection occurs when there is a common element; hence the number of such pairs is given by:

   $$ n((R \times T) \cap (T \times R)) = n(R \cap T) = 2. $$

3. Evaluate $n(P(R × R) ∩ (T × T))$

   The power set $P(R)$ has $2^{n(R)} = 2^3 = 8$ subsets. The Cartesian product $R \times R$ consists of $3 \times 3 = 9$ pairs, and similarly for $T \times T$ it has $6 \times 6 = 36$. The intersection requires finding common pairs in the power set, which doesn't yield a numeric intersection in this context. Thus,

   $$ n(P(R \times R) \cap (T \times T)) = 0 \text{ (no pairs in common)}. $$

4. Calculate $n((R × T) ∪ (T × R))$

   First find:

   • $n(R × T) = n(R) \times n(T) = 3 \times 6 = 18$
   • $n(T × R) = n(T) \times n(R) = 6 \times 3 = 18$

   Since both are disjoint, we add them together:

   $$ n((R \times T) \cup (T \times R)) = n(R \times T) + n(T \times R) = 18 + 18 = 36. $$

5. Calculate $n(R ∪ T)$

   This is already given as:

   $$ n(R ∪ T) = 7 $$