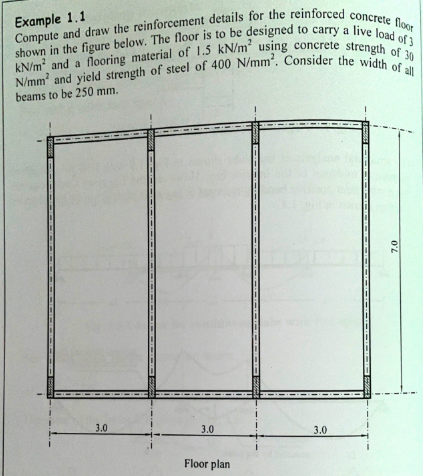
Compute and draw the reinforcement details for the reinforced concrete floor as shown in the figure. The floor is to be designed to carry a live load of 3 kN/m² and a flooring mate... Compute and draw the reinforcement details for the reinforced concrete floor as shown in the figure. The floor is to be designed to carry a live load of 3 kN/m² and a flooring material of 1.5 kN/m² using concrete strength of 30 N/mm² and yield strength of steel of 400 N/mm². Consider the width of all beams to be 250 mm.
Understand the Problem
The question is asking to compute and draw the reinforcement details for a reinforced concrete floor based on the given parameters such as loads, material strengths, and beam width. This involves calculations to ensure the design meets structural requirements.
Answer
The required area of steel reinforcement is approximately \(51.1 \, \text{mm}^2\). Use at least one 16 mm diameter bar.
Answer for screen readers
The required area of steel reinforcement is approximately (51.1 , \text{mm}^2). Use at least one 16 mm diameter bar for the design.
Steps to Solve
-
Determine Total Load on the Floor
Calculate the total load on the floor by summing the live load and the dead load:
- Live load = ( 3 , \text{kN/m}^2 )
- Dead load = ( 1.5 , \text{kN/m}^2 )
Total load ($w$) can be calculated as:
$$ w = \text{Live load} + \text{Dead load} = 3 + 1.5 = 4.5 , \text{kN/m}^2 $$
-
Calculate Load on Each Beam
Each beam supports a portion of the floor area. Given the floor dimensions (width = 3 m, length = 7 m, and beam spacing = 3 m), we find the contribution to the beam based on the tributary area:
Each beam supports:
$$ \text{Load on Each Beam} = w \times \text{Width of Beam} \times \text{Length of Beam} $$
Here:
Width of beam = 0.25 m (250 mm)
$$ \text{Load} = 4.5 \times 0.25 \times 7 = 7.875 , \text{kN} $$
-
Calculate Bending Moment at Midspan
The maximum bending moment ($M$) for a simply supported beam can be calculated using the formula:
$$ M = \frac{wL^2}{8} $$
Substituting in the values:
$$ M = \frac{7.875 \times (3)^2}{8} = \frac{7.875 \times 9}{8} = 8.859375 , \text{kN} \cdot \text{m} $$
-
Determine Required Area of Steel Reinforcement
Using the bending moment, we can find the required area of steel reinforcement ($A_s$) using:
$$ A_s = \frac{M}{0.87 f_y d} $$
Here,
- (f_y = 400 , \text{N/mm}^2)
- Effective depth ($d$) is assumed to be about 0.5 m (500 mm).
Therefore:
$$ A_s = \frac{8.859375 \times 10^6}{0.87 \times 400 \times 500} \approx 51.1 , \text{mm}^2 $$
-
Select Reinforcement Bars
After calculating the area needed, select appropriate rebar sizes. For instance, use 16 mm diameter bars with an area of ( \approx 201 , \text{mm}^2) for each.
- Number of bars required:
$$ \text{Number of bars} = \frac{A_s}{\text{Area of one bar}} = \frac{51.1}{201} \approx 0.25 $$
You would typically round up to use at least one bar.
The required area of steel reinforcement is approximately (51.1 , \text{mm}^2). Use at least one 16 mm diameter bar for the design.
More Information
This reinforcement design is essential for structural integrity, ensuring that the beam can withstand the calculated loads without failing. Selecting the appropriate bar size helps distribute the forces evenly and maintain safety standards.
Tips
- Failing to properly account for both live and dead loads when calculating total load.
- Miscalculating the bending moment due to an incorrect interpretation of beam conditions (simply supported, fixed, etc.).
- Neglecting to check the effective depth of the beam while calculating the area of steel required.
AI-generated content may contain errors. Please verify critical information