Complete the square to re-write the quadratic function in vertex form: y = x² + 4x - 2
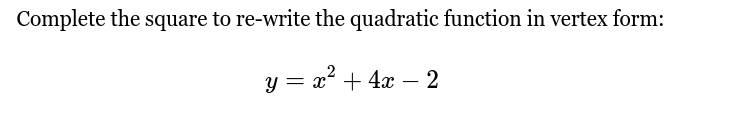
Understand the Problem
The question asks to complete the square for the quadratic function given, which involves transforming it into vertex form. This will typically be done by manipulating the equation to express it in the form y = a(x-h)² + k, where (h, k) is the vertex of the parabola.
Answer
The vertex form is \( y = (x + 2)^2 - 4 \).
Answer for screen readers
The quadratic function in vertex form is ( y = (x + 2)^2 - 4 ).
Steps to Solve
-
Identify the coefficients The quadratic function is given as ( y = x^2 + 4x - 2 ). Here, the coefficient of ( x^2 ) is 1, and the coefficient of ( x ) is 4.
-
Group the quadratic and linear terms We need to complete the square for the expression ( x^2 + 4x ): $$ y = (x^2 + 4x) - 2 $$
-
Find the value to complete the square Take half of the linear coefficient (4) and square it. Half of 4 is 2, and squaring this gives us: $$ 2^2 = 4 $$
-
Add and subtract this value inside the group To keep the equation balanced, add and subtract 4 inside the parenthesis: $$ y = (x^2 + 4x + 4 - 4) - 2 $$
-
Rewrite the expression in vertex form Now, factor the perfect square trinomial and simplify: $$ y = (x + 2)^2 - 4 $$
-
Final form Thus, the function in vertex form is: $$ y = (x + 2)^2 - 4 $$
The quadratic function in vertex form is ( y = (x + 2)^2 - 4 ).
More Information
Completing the square repositions the vertex of the parabola represented by the quadratic equation. In this case, the vertex is ((-2, -4)). This method is widely used in calculus and optimization problems.
Tips
- Forgetting to balance the equation: When adding a square completion value, remember to subtract the same value to maintain equality.
- Incorrectly squaring half the coefficient: Always ensure to correctly calculate half the coefficient before squaring it.
AI-generated content may contain errors. Please verify critical information