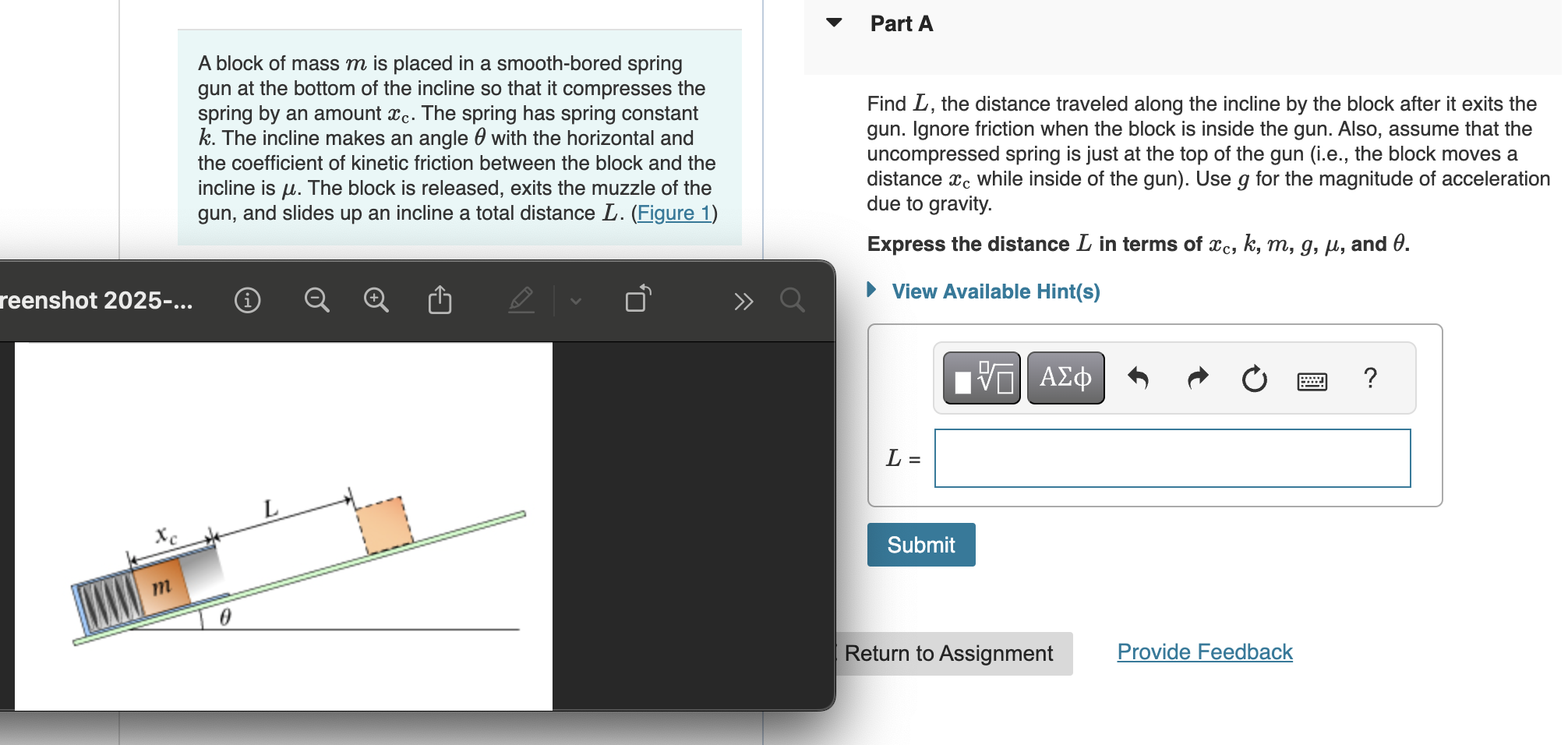
Find L, the distance traveled along the incline by the block after it exits the gun. Ignore friction when the block is inside the gun. Assume that the uncompressed spring is just a... Find L, the distance traveled along the incline by the block after it exits the gun. Ignore friction when the block is inside the gun. Assume that the uncompressed spring is just at the top of the gun. Express the distance L in terms of xc, k, m, g, μ, and θ. Read more

Steps to Solve

1. Energy Conservation in the Spring When the block is compressed in the spring, the potential energy stored in the spring is given by:

$$ PE_{spring} = \frac{1}{2} k x_c^2 $$

This energy converts into kinetic energy as it exits the spring.

2. Kinetic Energy of the Block Upon exiting the spring, the total kinetic energy of the block can be expressed as:

$$ KE = \frac{1}{2} m v^2 $$

Setting the spring potential energy equal to the kinetic energy gives us:

$$ \frac{1}{2} k x_c^2 = \frac{1}{2} m v^2 $$

From this, we can solve for the velocity ( v ):

$$ v = \sqrt{\frac{k}{m}} x_c $$

3. Forces Acting on the Block After Exiting the Spring After exiting the spring, the block experiences two forces: gravitational force down the incline and frictional force opposing the motion. The gravitational force down the incline is:

$$ F_{gravity} = m g \sin \theta $$

The kinetic friction force opposing the motion is:

$$ F_{friction} = \mu m g \cos \theta $$

4. Net Force and Acceleration The net force acting on the block is:

$$ F_{net} = F_{gravity} - F_{friction} = m g \sin \theta - \mu m g \cos \theta $$

Using Newton's second law ( F = ma ):

$$ m a = m g \sin \theta - \mu m g \cos \theta $$

Canceling ( m ):

$$ a = g (\sin \theta - \mu \cos \theta) $$

5. Using Kinematic Equation for Distance L To find the distance ( L ) traveled by the block before coming to rest, we can use the kinematic equation:

$$ v_f^2 = v_i^2 + 2aL $$

Since the final velocity ( v_f = 0 ):

$$ 0 = v^2 + 2aL $$

Rearranging gives us:

$$ L = \frac{-v^2}{2a} $$

Substituting in the previously found expressions for ( v ) and ( a ):

$$ L = \frac{-\left(\sqrt{\frac{k}{m}} x_c\right)^2}{2\left(g( \sin \theta - \mu \cos \theta)\right)} $$

This simplifies to:

$$ L = \frac{-\frac{k}{m} x_c^2}{2g(\sin \theta - \mu \cos \theta)} $$

Since ( L ) must be positive, we take the absolute value:

$$ L = \frac{k x_c^2}{2mg(\sin \theta - \mu \cos \theta)} $$