Complete the square to re-write the quadratic function in vertex form: y = x² + 5x + 4
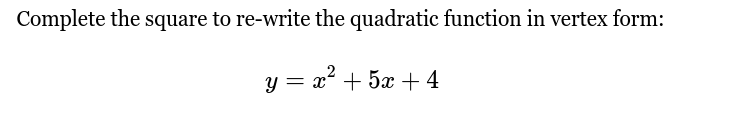
Understand the Problem
The question is asking to complete the square of the given quadratic function to rewrite it in vertex form. The high-level approach involves rewriting the quadratic expression and identifying the vertex.
Answer
The vertex form of the quadratic function is $$ y = \left(x + \frac{5}{2}\right)^2 - \frac{9}{4} $$
Answer for screen readers
The quadratic function in vertex form is
$$ y = \left(x + \frac{5}{2}\right)^2 - \frac{9}{4} $$
Steps to Solve
- Identify the quadratic expression We start with the quadratic function given by:
$$ y = x^2 + 5x + 4 $$
- Group the quadratic and linear terms Separate the quadratic and linear terms from the constant:
$$ y = (x^2 + 5x) + 4 $$
- Complete the square for the expression inside the parentheses To complete the square, take half of the coefficient of $x$ (which is 5), square it, and add/subtract it inside the parentheses:
- Half of 5 is $\frac{5}{2}$.
- Squaring it gives $\left( \frac{5}{2} \right)^2 = \frac{25}{4}$.
Now add and subtract this square inside the parentheses:
$$ y = \left(x^2 + 5x + \frac{25}{4} - \frac{25}{4}\right) + 4 $$
- Rewrite the expression Now, rewrite the square and combine the constants:
$$ y = \left(x + \frac{5}{2}\right)^2 - \frac{25}{4} + 4 $$
To combine the constants, convert 4 into a fraction with a denominator of 4:
$$ 4 = \frac{16}{4} $$
Thus, we have:
$$ -\frac{25}{4} + \frac{16}{4} = -\frac{9}{4} $$
- Final vertex form Now substitute back into the equation:
$$ y = \left(x + \frac{5}{2}\right)^2 - \frac{9}{4} $$
This is the vertex form of the quadratic function.
The quadratic function in vertex form is
$$ y = \left(x + \frac{5}{2}\right)^2 - \frac{9}{4} $$
More Information
The vertex of the quadratic function is located at the point $\left(-\frac{5}{2}, -\frac{9}{4}\right)$. This form makes it easy to identify the vertex of the parabola and helps in graphing quadratic functions.
Tips
- Forgetting to combine the constant terms properly; ensure that the fractions are over the same denominator before combining.
- Not squaring half of the linear coefficient accurately; remember to perform the squaring step correctly.
AI-generated content may contain errors. Please verify critical information