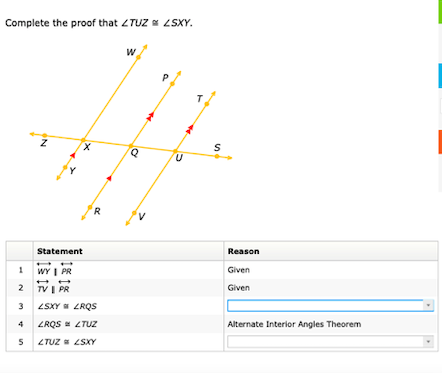
Complete the proof that angle TUZ is congruent to angle SXY.
Understand the Problem
The question is asking to complete a proof showing that angle TUZ is congruent to angle SXY. It provides a partially completed proof with a structure that includes statements and reasons, likely related to properties of parallel lines and angles formed by transversals.
Answer
The angles are congruent: $\angle TUZ \cong \angle SXY$.
Answer for screen readers
The final answer is that $\angle TUZ \cong \angle SXY$.
Steps to Solve
-
Identify Parallel Lines The problem states that line segments $WY$ and $PR$ are parallel. This means that angles formed by a transversal crossing these lines will maintain specific angle relationships.
-
Apply Alternate Interior Angles Theorem Since $WY \parallel PR$, we can say that angle $SXY$ is congruent to angle $LRS$ based on the Alternate Interior Angles Theorem. Thus, we can write: $$ \angle SXY \cong \angle LRS $$
-
Use Transitive Property of Congruence Next, since $\angle LRS \cong \angle TUZ$ from the existing proof steps, we can apply the transitive property of congruence. This means we can say: $$ \angle SXY \cong \angle TUZ $$
-
Conclusively State Final congruence By combining the congruence statements from the previous step, we conclude that: $$ \angle TUZ \cong \angle SXY $$
The final answer is that $\angle TUZ \cong \angle SXY$.
More Information
This proof utilizes properties of parallel lines, particularly the Alternate Interior Angles Theorem, which states that if two parallel lines are cut by a transversal, each pair of alternate interior angles is congruent. This property is foundational in geometric proofs.
Tips
- Not identifying the correct pairs of congruent angles. When using the Alternate Interior Angles Theorem, ensure that the angles being referenced are indeed alternate interior angles.
- Failing to state the transitive property. Whenever you deduce further congruence from previously established angles, it's essential to cite that property.
AI-generated content may contain errors. Please verify critical information