Combine like terms: 7y^3 - 7x^3 + 4 - 5 + 6 - 3x^3 + 6x^3.
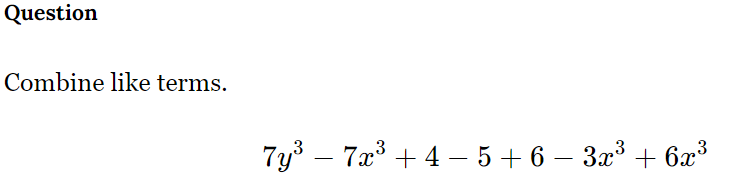
Understand the Problem
The question is asking us to combine like terms from the given polynomial expression. We will identify and group the terms that share the same variable and exponent, and then simplify the expression accordingly.
Answer
The combined expression is $7y^3 - 4x^3 + 5$.
Answer for screen readers
The combined expression is:
$$ 7y^3 - 4x^3 + 5 $$
Steps to Solve
- Identify Like Terms
First, we will identify the like terms in the given polynomial expression:
- The $y^3$ term: $7y^3$
- The $x^3$ terms: $-7x^3$, $-3x^3$, and $6x^3$
- The constant terms: $4$, $-5$, and $6$
- Combine Like Terms for $y^3$
There is only one $y^3$ term:
$$ 7y^3 $$
So it remains as $7y^3$.
- Combine Like Terms for $x^3$
Now we will combine the $x^3$ terms:
$$ -7x^3 - 3x^3 + 6x^3 $$
Calculating this gives:
$$ (-7 - 3 + 6)x^3 = -4x^3 $$
- Combine Constant Terms
Next, we will combine the constant terms:
$$ 4 - 5 + 6 $$
Calculating this gives:
$$ (4 - 5 + 6) = 5 $$
- Write the Final Expression
Now we can combine all the results we've calculated:
$$ 7y^3 - 4x^3 + 5 $$
The combined expression is:
$$ 7y^3 - 4x^3 + 5 $$
More Information
Combining like terms is a fundamental concept in algebra that helps simplify polynomial expressions. Each term is grouped based on similar variables and exponents, allowing for easier manipulation in equations.
Tips
- Forgetting to combine all like terms: Ensure that all instances of each variable and constants are considered.
- Miscalculating the sums or differences while combining constants: Carefully double-check arithmetic operations.