Combine like terms: -7y^3 - 3y + 5y - y^3 - 4 + 7y^3 - 7y.
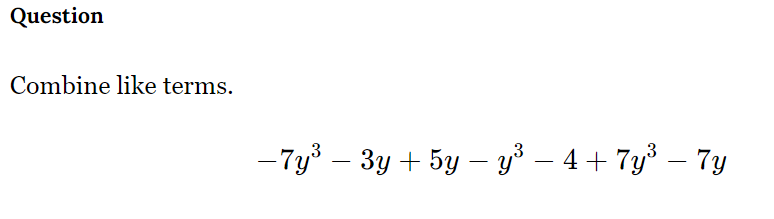
Understand the Problem
The question is asking to combine like terms in the provided polynomial expression involving terms with different powers of y. The goal is to simplify the expression by summing the coefficients of like terms.
Answer
The simplified expression is $-8y^3 - 6y - 4$.
Answer for screen readers
The simplified expression is $-8y^3 - 6y - 4$.
Steps to Solve
-
Identify Like Terms
Review the expression to find terms with the same power of $y$.The terms are:
- For $y^3$: $-7y^3$, $-y^3$, $7y^3$, $-7y^3$
- For $y$: $-3y$, $5y$, $-y$, $-7y$
- For constants: $-4$
-
Combine Like Terms for $y^3$
Sum the coefficients of the $y^3$ terms: $$ -7 + (-1) + 7 + (-7) = -8 $$ Thus, the combined $y^3$ term is $-8y^3$. -
Combine Like Terms for $y$
Sum the coefficients of the $y$ terms: $$ -3 + 5 + (-1) + (-7) = -6 $$ Thus, the combined $y$ term is $-6y$. -
Combine Constant Terms
There is only one constant term: $$-4$$ -
Write the Final Combined Expression
Combine all simplified terms into a single expression: $$ -8y^3 - 6y - 4 $$
The simplified expression is $-8y^3 - 6y - 4$.
More Information
This expression represents a polynomial that has been reduced by combining like terms, making it simpler to work with or analyze further. Combining like terms is a fundamental skill in algebra that helps streamline expressions and equations.
Tips
- Misidentifying Like Terms: Ensure that only terms with the same variable and power are combined.
- Incorrect Sign Handling: Be careful with the signs (positive and negative) when summing coefficients.
AI-generated content may contain errors. Please verify critical information